题目内容
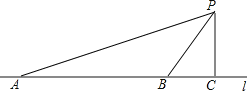
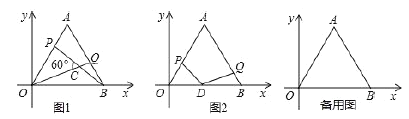
【题目】如图,在平面直角坐标系中,![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标
的坐标![]() ,点
,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,过点
上位于第二象限内的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,记点
,记点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)若![]() ,求
,求![]() 点的坐标.
点的坐标.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设直线AB解析式为![]() ,把A和B的坐标代入求出k和b的值,即可求出解析式;
,把A和B的坐标代入求出k和b的值,即可求出解析式;
(2)由![]() 以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得到P点横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标.
以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得到P点横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标.
解:(1)设直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() 两点,
两点,
∴![]() 解得:
解得:
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)如解图所示,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,

∵当![]() 时,
时,![]() 为等腰三角形,而
为等腰三角形,而![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]()
∴![]() ,
,
∴![]() ,
,
∵点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,
,
∴![]() ,
,
∵点![]() 是直线
是直线![]() 上位于第二象限内的一个点,
上位于第二象限内的一个点,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目
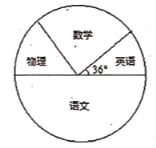
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |
(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.