题目内容
16.已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为$\frac{5}{3}$cm.分析 根据勾股定理求出斜边的长度,根据斜边中线长为斜边长的一半求出斜边的中线CD,由重心定理即可得出GD的长.
解答 解:如图所示:连接CD,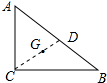
∵∠ACB=90°,
∴斜边AB=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm),
∴斜边AB的中线CD=$\frac{1}{2}$×10=5(cm),
∵D为Rt△ABC的外心,G是重心,
∴由重心定理得:GD=$\frac{1}{3}$CD=$\frac{5}{3}$(cm).
故答案为:$\frac{5}{3}$cm.
点评 本题考查了勾股定理、直角三角形斜边上的中线性质、重心定理;熟练掌握勾股定理和重心定理,熟记直角三角形的外心是斜边的中点是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.根据下面的两种移动电话计费方式表,考虑下列问题.
(1)设本地通话时间为x,请列代数式说明按两种方式如何计算?
(2)在本地通话时间相同的条件下,请你帮助用户选择哪种方式更省钱?
| 方式一 | 方式二 | |
| 月租费 | 50元/月 | 10元/月 |
| 本地通话费 | 0.30元/分 | 0.5元/分 |
(2)在本地通话时间相同的条件下,请你帮助用户选择哪种方式更省钱?