题目内容
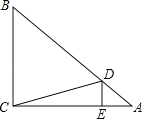
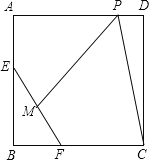
【题目】如图,![]() 中,以
中,以![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,交
,交![]() 于点
于点![]() .
.

(1)若![]() ,求证:
,求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(3)在(2)的条件下,若![]() ,求⊙
,求⊙![]() 的半径.
的半径.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)根据AB为⊙![]() 直径,得出
直径,得出![]() =90°,即
=90°,即![]() °,
°,![]() ,
,![]() ,推出
,推出![]() ,即
,即![]() °,
°,
所以![]() =
=![]() =90°,得出AC为⊙
=90°,得出AC为⊙![]() 的切线;(2)证明
的切线;(2)证明![]() , 得到
, 得到![]() ,因为
,因为![]() ,所以
,所以![]() ,即可得到AE平分
,即可得到AE平分![]() ;(3)过点F作FH⊥AB于H可证
;(3)过点F作FH⊥AB于H可证![]() ,可得AH=AD=4,FH=DF=2;可证
,可得AH=AD=4,FH=DF=2;可证![]() 故
故![]() ;BH=x,则BD=2x,BF=2x-2,利用勾股定理可得
;BH=x,则BD=2x,BF=2x-2,利用勾股定理可得![]() ,
,![]() ;解得BH=
;解得BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ,由AO=
,由AO=![]() AB=
AB=![]() ,即可得⊙
,即可得⊙![]() 的半径.
的半径.
(1)证明:∵AB为⊙![]() 直径,
直径,
∴![]() =90°,
=90°,
∴![]() °,
°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() °,
°,
即![]() °,
°,
∴AC为⊙![]() 的切线;
的切线;
(2)证明:∵![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
即AE平分![]() .
.
(3)解:过点F作FH⊥AB于H.
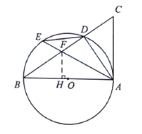
∴![]() °;
°;
又∵![]() ,AF=AF,
,AF=AF,
∴![]() ;
;
∴AH=AD=4,FH=DF=2;
∵![]() °,
°,![]() ,
,
∴![]() ,
,
∴![]() ;
;
设BH=x,则BD=2x,BF=2x-2,
∴![]() ,
,
∴![]() ;
;
∴x=0(舍)或x=![]() ;
;
∴BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ;
;
∴AO=![]() AB=
AB=![]() ;
;
∴⊙![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目