题目内容
5.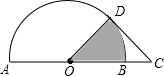 如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.
如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.
分析 根据已知条件证得三角形ODC是等腰直角三角形,得到∠DOB=45°,然后根据扇形的面积公式计算即可.
解答 解:∵ AB为半圆O的直径,
AB为半圆O的直径,
∴AB=2OD,
∵AB=2CD=4,
∴OD=CD=2,
∵CD与半圆O相切于点D,
∴∠ODC=90°,
∴∠DOB=45°,
∴阴影部分的面积=$\frac{45π•{2}^{2}}{360}$=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题考查了切线的性质,扇形的面积的求法,等腰直角三角形的性质,证得△ODC是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
16.记A=$\sum_{k=1}^{2013}$$\sqrt{1+\frac{1}{{k}^{2}}+\frac{1}{(k+1)^{2}}}$,再记[A]表示不超过A的最大整数,则[A]( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 2013 |
13. 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
 如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )
如图,菱形ABCD中,AC=16,BD=12,则菱形的周长是( )| A. | 20 | B. | 24 | C. | 28 | D. | 40 |
 已知:在梯形ABCD中,AD∥BC,E、F分别是BD、AC中点,求证:EF∥BC,EF=$\frac{1}{2}$(BC-AD).
已知:在梯形ABCD中,AD∥BC,E、F分别是BD、AC中点,求证:EF∥BC,EF=$\frac{1}{2}$(BC-AD). 如图,字每个小正方形的边长为1个长度单位的长方形网格中,有一个△ABC
如图,字每个小正方形的边长为1个长度单位的长方形网格中,有一个△ABC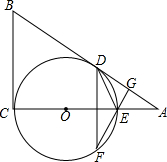 如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.
如图,已知AB和BC分别与圆O相切于点D、C,AC经过圆心O交圆于点E,AC=2AD且BD=2.