题目内容
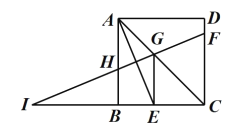
【题目】如图,在![]() 中,
中,![]() 为斜边
为斜边![]() 的中线,过点D作
的中线,过点D作![]() 于点E,延长
于点E,延长![]() 至点F,使
至点F,使![]() ,连接
,连接![]() ,点G在线段
,点G在线段![]() 上,连接
上,连接![]() ,且
,且![]() .下列结论:①
.下列结论:①![]() ;②四边形
;②四边形![]() 是平行四边形;③
是平行四边形;③![]() ;④
;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
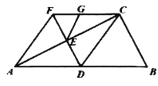
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据直角三角形的性质知DA=DB=DC,根据等腰三角形的性质结合菱形的判定定理可证得四边形ADCF为菱形,继而推出四边形DBCF为平行四边形,可判断①②;利用邻补角的性质结合已知可证得∠CFE =∠FGE,即可判断③;由③的结论可证得△FEG![]() △FCD,推出
△FCD,推出![]() ,即可判断④.
,即可判断④.
∵在![]() 中,
中,![]() 为斜边
为斜边![]() 的中线,
的中线,
∴DA=DB=DC,
∵![]() 于点E,且
于点E,且![]() ,
,
∴AE=EC,
∴四边形ADCF为菱形,
∴FC∥BD,FC=AD=BD,
∴四边形DBCF为平行四边形,故②正确;
∴DF=BC,
∴DE=![]() BC,故①正确;
BC,故①正确;
∵四边形ADCE为菱形,

∴CF=CD,
∴∠CFE=∠CDE,
∵∠CDE+∠EGC=180![]() ,而∠FGE+∠EGC=180
,而∠FGE+∠EGC=180![]() ,
,
∴∠CDE=∠FGE,∠CFE =∠FGE,
∴EF=EG,故③正确;
∵∠CDF=∠FGE,∠CFD=∠EFG,
∴△FEG![]() △FCD,
△FCD,
∴![]() ,即
,即 ,
,
∴![]() ,
,
∴BC =DF![]() ,故④正确;
,故④正确;
综上,①②③④都正确,
故选:D.

练习册系列答案
相关题目