题目内容
已知，如图，斜坡PQ坡度为i=1：| 4 | 3 |
8米
8米
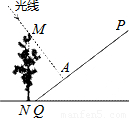
．分析：此题是把实际问题转化为解直角三角形问题，由已知作图，由已知得Rt△CAQ和Rt△MBC，BC=NQ=1米，BN=CQ，tan∠ACQ=tan∠BMC=1：
，由三角函数可求出AC、CQ、BM，从而求出大树MN的高度．
| 4 |
| 3 |
解答：解：由已知得图：
则得Rt△CAQ和Rt△MBC，BC=NQ=1米，BN=CQ，
tan∠ACQ=tan∠BMC=1：
=
，
∴AC=
=
=
，
∴CQ=
=
=
，
∴BN=
，
∴BM=
=
=
，
∴MN=BN+BM=
+
=8，
故答案为：8米．
则得Rt△CAQ和Rt△MBC，BC=NQ=1米，BN=CQ，
tan∠ACQ=tan∠BMC=1：
| 4 |
| 3 |
| 3 |
| 4 |
∴AC=
| AQ |
| tan∠ACQ |
| 4 | ||
|
| 16 |
| 3 |
∴CQ=
| AC2+AQ2 |
(
|
| 20 |
| 3 |
∴BN=
| 20 |
| 3 |
∴BM=
| BC |
| tan∠BMC |
| 1 | ||
|
| 4 |
| 3 |
∴MN=BN+BM=
| 20 |
| 3 |
| 4 |
| 3 |
故答案为：8米．
点评：此题考查的知识点是解直角三角形的应用问题，解答此题的关键是把实际问题转化为解直角三角形问题由已知得Rt△CAQ和Rt△MBC，tan∠ACQ=tan∠BMC=1：
．
| 4 |
| 3 |
练习册系列答案
阅读快车系列答案
相关题目
为原点，OA所在直线为y轴，过O点垂直于OA的直线为x轴建立直角坐标系．设水喷到斜坡上的最低点为B，最高点为C．
，在坡面上点O处有一根1m高且垂直于水平面的水管OA，顶端A处有一旋转式喷头向外喷水，水流在各个方向沿相同的抛物线落下，水流最高点M比点A高出1m，且在点A测得点M的仰角为30°，以O点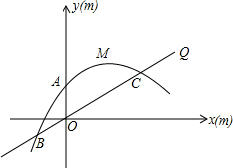
为原点，OA所在直线为y轴，过O点垂直于OA的直线为x轴建立直角坐标系．设水喷到斜坡上的最低点为B，最高点为C．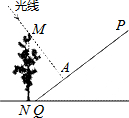
，坡脚Q旁的点N处有一棵大树MN．近中午的某个时刻，太阳光线正好与斜坡PQ垂直，光线将树顶M的影子照射在斜坡PQ上的点A处．如果AQ=4米，NQ=1米，则大树MN的高度为 ．