Question

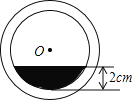
【题目】将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水部分的面积是（　　）

A.（π﹣4）cm2B.（π﹣8）cm2

C.（π﹣4）cm2D.（π﹣2）cm2

Answer 1

【答案】A

【解析】

作OD⊥AB于C，交小圆于D，则CD＝2，由垂径定理可知AC＝CB，利用正弦函数求得∠OAC＝30°，进而求得∠AOB＝120°，利用勾股定理即可求出AB的值，从而利用S扇形S△AOB求得杯底有水部分的面积．

解：作OD⊥AB于C，交小圆于D，则CD＝2，AC＝BC，

∵OA＝OD＝4，CD＝2，

∴OC＝2，

在Rt△AOC中，sin∠OAC＝＝，

∴∠OAC＝30°，

∴∠AOC＝60°，

∴∠AOB＝120°，AC＝，

∴AB＝，

∴杯底有水部分的面积＝S扇形﹣S△AOB＝cm2，

故选：A．