题目内容
如图所示，四边形ABCD是正方形，点E是边CD上一点，点F是CB延长线上一点，且 DE=BF，通过观察，回答下列问题：
(1)△AFB可以看作是哪个三角形绕哪一个点旋转多少度得到的图形?
(2)△AEF是什么形状的三角形?请说明你的理由，即证明。
解：（1）△AFB可以看作是△AED绕点A顺时针旋转90°得到；
（2）∵AD=AB，∠D=∠ABF，DE=BF，
∴△ADE≌△ABF，
∴AE=AF，∠DAE=∠BAF，
∴∠EAF∠BAE+∠BAF=∠BAE+∠DAE=∠DAB=90°，
所以△AEF是等腰直角三角形
天天向上一本好卷系列答案
小学生10分钟应用题系列答案某公司有
型产品40件，
型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完．两商店销售这两种产品每件的利润（元）如下表：
|
|
| |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
（1）设分配给甲店型产品
件，这家公司卖出这100件产品的总利润为W（元），请用X的关系式来表示W，并求出的取值范围；
（2）若公司要求总利润不低于17560元，说明有多少种不同分配方案，并将各种方案设计出来；
（3）为了促销，公司决定仅对甲店型产品让利销售，每件让利
元，但让利后型产品的
件利润仍高于甲店型产品的每件利润．甲店的型产品以及乙店的
型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大？
的长方形场地，求这个长方形场地的两边长，设墙的对边长为
，可列方程为 ( )
B．
D．
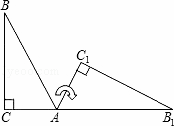
.如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角等于（ ）
|
| A． | 55° | B． | 125° | C． | 70° | D． | 145° |
B.
C.
D.
未成年人思想道德建设越来越受到社会的关注．某青少年研究所随机调查了市内某校100名学生寒假中花零花钱的数量（钱数取整数．单位：元）以便引导学生树立正确的消费观．根据调查数据制成了频率分布表和直方图（如图）
（1）补全频率分布表；
（2）在频率分布直方图中长方形ABCD的面积是________．这次调查的样本容量是______；
（3）研究所认为，应对消费150元以上的学生提出勤俭节约的建议．试估计应对该校1000 名学生中约多少名学生提出这项建议?
分组 | 频数 | 频率 |
0.5～50.5 | 0．1 | |
50.5～ | 20 | 0．2 |
100.5～150.5 | ||
～200.5 | 30 | 0．3 |
200.5～250.5 | 10 | 0．1 |
250.5～300.5 | 5 | 0．05 |
合计 | 100 |