题目内容
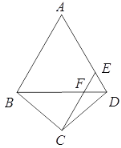
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,
,![]() .
. ![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ∥
∥![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() . 求
. 求![]() 的长 .
的长 .
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由等边三角形的判定定理可得△ABD为等边三角形,又由平行进行角度间的转化可得出结论.
(2)连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.
(1)证明:∵![]() ,
,![]() ,
,
∴△![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() .
.
(2)解:连接![]() 交
交![]() 于点
于点![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() .
.
∵△![]() 是等边三角形,
是等边三角形,![]()
∴![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]() ,
, ![]() .
.
∵![]() .
.
∴![]() .
.
∴△![]() 是等边三角形.
是等边三角形.
∴![]() ,
,
∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.
在Rt△![]() 中,
中,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目