题目内容
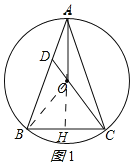
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.

【答案】(1)证明见解析;(2)AC=![]() , CD=
, CD=![]() ,
,
【解析】分析:(1)延长AO交BC于H,连接BO,证明A、O在线段BC的垂直平分线上,得出AO⊥BC,再由等腰三角形的性质即可得出结论;(2)延长CD交⊙O于E,连接BE,则CE是⊙O的直径,由圆周角定理得出∠EBC=90°,∠E=∠BAC,得出sinE=sin∠BAC,求出CE=![]() BC=10,由勾股定理求出BE=8,证出BE∥OA,得出
BC=10,由勾股定理求出BE=8,证出BE∥OA,得出![]() ,求出OD=
,求出OD=![]() ,得出CD=
,得出CD=![]() ,而BE∥OA,由三角形中位线定理得出OH=
,而BE∥OA,由三角形中位线定理得出OH=![]() BE=4,CH=
BE=4,CH=![]() BC=3,在Rt△ACH中,由勾股定理求出AC的长即可.
BC=3,在Rt△ACH中,由勾股定理求出AC的长即可.
本题解析:
解:(1)证明:延长AO交BC于H,连接BO.
∵AB=AC,OB=OC,
∴A,O在线段BC的垂直平分线上.∴AO⊥BC.
又∵AB=AC,∴AO平分∠BAC.
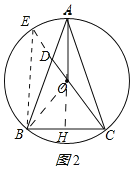
(2)延长CD交⊙O于E,连接BE,则CE是⊙O的直径.
∴∠EBC=90°,BC⊥BE.
∵∠E=∠BAC,∴sinE=sin∠BAC.
∴![]() =
=![]() .∴CE=
.∴CE=![]() BC=10.
BC=10.
∴BE=![]() =8,OA=OE=
=8,OA=OE=![]() CE=5.
CE=5.
∵AH⊥BC,∴BE∥OA.
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得OD=![]() .∴CD=5+
.∴CD=5+![]() =
=![]() .
.
∵BE∥OA,即BE∥OH,OC=OE,∴OH是△CEB的中位线.
∴OH=![]() BE=4,CH=
BE=4,CH=![]() BC=3.∴AH=5+4=9.
BC=3.∴AH=5+4=9.
在Rt△ACH中,AC=![]() =
=![]() =3
=3![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

