题目内容
7.在菱形ABCD中,∠ABC=60°,(1)如图(1),AC、BD相交于点O,延长BC到点E,使得CE=AO,若AB=2,求OE的长;
(2)如图(2),点P在AC延长线上,点E在BC延长线上,若AP=CE,求证:BP=EP
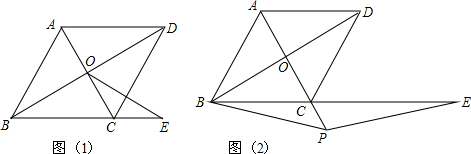
分析 (1)证明△ABC是等边三角形,得出∠ACB=60°=∠E+∠EOC,证出OB=OE,由三角函数求出OB,即可得出OE的长;
(2)先由SAS证明△ABP≌△CDE,得出BP=DE,∠ABP=∠CDE,再由SAS证明△BCP≌△DCP,得出DP=BP,∠CBP=∠CDP,得出DP=DE,然后证明△DPE是等边三角形,即可得出结论.
解答 (1)解:∵四边形ABCD为菱形,∠ABC=60°,
∴AB=BC,AC⊥BD,AO=CO,∠ABO=∠OBC=$\frac{1}{2}$∠ABC=30°,
∵CE=AO,
∴CE=CO,
∴∠E=∠EOC,
∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,
∴∠ACB=60°=∠E+∠EOC,
∴∠E=∠EOC=30°=∠OBC,
∴OB=OE,
∵AB=2,∠ABO=30°,
∴OB=AB•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴OE=$\sqrt{3}$;
(2)证明:连接DP、DE,如图所示: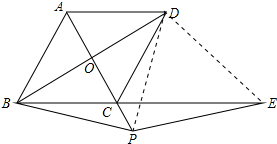
∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,AD∥BC,∠BAC=∠DAC,
∴∠DCE=∠ABC=60°,∠BAD+∠ABC=180°,
∴∠BAD=180°-∠ABC=120°,
∴∠BAC=60°,
∴∠BAC=∠DCE,
在△ABP和△CDE中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠BAC=∠DCE}&{\;}\\{AP=CE}&{\;}\end{array}\right.$,
∴△ABP≌△CDE(SAS),
∴BP=DE,∠ABP=∠CDE,
又∵AC平分∠DCB,
∴∠ACB=∠ACD=60°,
∴∠BCP=∠DCP=120°,
在△BCP和△DCP中,$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCP=∠DCP}&{\;}\\{CP=CP}&{\;}\end{array}\right.$,
∴△BCP≌△DCP(SAS)
∴DP=BP,∠CBP=∠CDP,
∴DP=DE,
∠CDE-∠CDP=∠ABP-∠CBP,
即∠EDP=∠ABC=60°,
∴△DPE是等边三角形,
∴DE=PE,
∴BP=EP.
点评 本题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质;本题综合性强,有一定难度,特别是(2)中,需要两次证明三角形全等才能得出结论.

| A. | xy+x=y | B. | x2=-1 | C. | ax2+bx=0 | D. | (x-5)x=x2-2x-1 |
| A. | 三条边对应相等 | B. | 两条边及其夹角对应相等 | ||
| C. | 两角和一条边对应相等 | D. | 两条边和一条边所对的角对应相等 |
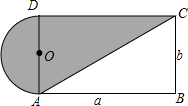 设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,
设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,