题目内容
已知tanα=
,则锐角α的取值范围是( )
| 6 |
| 5 |
分析:分别求出tan30°=
≈0.644,tan45°=1,tan60°=
≈1.732,tanα=
=1.2,得出tan45°<tanα<tan60°,根据根据正切值随角度的增大而增大即可得出答案.
| ||
| 3 |
| 3 |
| 6 |
| 5 |
解答:解:∵tan30°=
≈0.644,tan45°=1,tan60°=
≈1.732,
又∵tanα=
=1.2,
∴tan45°<tanα<tan60°,
∵锐角的正切值随角度的增大而增大,
∴45°<α<60°,
故选C.
| ||
| 3 |
| 3 |
又∵tanα=
| 6 |
| 5 |
∴tan45°<tanα<tan60°,
∵锐角的正切值随角度的增大而增大,
∴45°<α<60°,
故选C.
点评:本题考查了特殊角的三角函数值和锐角三角形函数的增减性的应用,主要考查学生的理解能力和判断能力,注意:锐角的正切值随角度的增大而增大.

练习册系列答案
相关题目
已知锐角α满足tan(α-20°)=1,则锐角α的值为( )
| A.50° | B.25° | C.45° | D.65° |
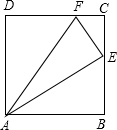 已知正方形ABCD中,AB=5,E是直线BC上的一点,连接AE,过点E作EF⊥AE,交直线CD于点F.
已知正方形ABCD中,AB=5,E是直线BC上的一点,连接AE,过点E作EF⊥AE,交直线CD于点F.