题目内容
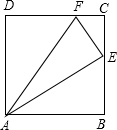 已知正方形ABCD中,AB=5,E是直线BC上的一点,连接AE,过点E作EF⊥AE,交直线CD于点F.
已知正方形ABCD中,AB=5,E是直线BC上的一点,连接AE,过点E作EF⊥AE,交直线CD于点F.(1)当E点在BC边上运动时,设线段BE的长为x,线段CF的长为y,
①求y关于x的函数解析式及其定义域;
②根据①中所得y关于x的函数图象,求当BE的长为何值时,线段CF最长,并求此时CF的长;
(2)当CF的长为
| 6 | 5 |
分析:(1)①由题意易得△CEF∽△BAE,根据对应边成比例,可得y关于x的函数解析式,根据BC的长确定定义域即可;
②用配方法求得二次函数的最值即可;
(2)因为tan∠EAF=EF:AE,则由①的函数解析式求得BE的值,由相似三角形对应边对应成比例,即可求得EF:AE=CF:BE.
②用配方法求得二次函数的最值即可;
(2)因为tan∠EAF=EF:AE,则由①的函数解析式求得BE的值,由相似三角形对应边对应成比例,即可求得EF:AE=CF:BE.
解答:解:(1)①∵四边形ABCD是正方形,
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=90°.
又∵∠CEA=∠CEF+∠AEF,∠CEA=∠BAE+∠B,
∴∠CEF=∠BAE.(1分)
又∵∠B=∠C=90°,
∴△CEF∽△BAE(1分)
∴
=
,
∴
=
,
∴y=-
x2+x(0<x<5);(2分)
②y=-
x2+x=-
(x-
)2+
(1分)
根据函数图象可知,抛物线y=-
(x-
)2+
,
开口向下,抛物线的顶点坐标是它的最高点、且x=
在函数的定义域内.
所以当BE的长为
时,CF的长最大为
(2分)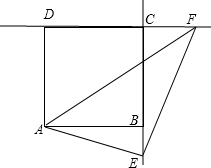
(2)若E在边BC上,CF=y=
,y=-
x2+x
∴-
x2+x-
=0,
解得x1=2,x2=3,
当BE=2时,tan∠EAF=
;
当BE=3,时tan∠EAF=
.
若E在CB延长线上时,同理可得△CEF∽△BAE,
∴
=
,即
=
,
∴y=
x2+x,
∵CF=y=
,
x2+x-
=0,
解得:x1=1,x2=-6(舍去),
当BE=1时,tan∠EAF=
.
当E点可在BC的延长线上,CE=1,
tan∠EAF=
.
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=90°.
又∵∠CEA=∠CEF+∠AEF,∠CEA=∠BAE+∠B,
∴∠CEF=∠BAE.(1分)
又∵∠B=∠C=90°,
∴△CEF∽△BAE(1分)
∴
| CF |
| BE |
| CE |
| AB |
∴
| y |
| x |
| 5-x |
| 5 |
∴y=-
| 1 |
| 5 |
②y=-
| 1 |
| 5 |
| 1 |
| 5 |
| 5 |
| 2 |
| 5 |
| 4 |
根据函数图象可知,抛物线y=-
| 1 |
| 5 |
| 5 |
| 2 |
| 5 |
| 4 |
开口向下,抛物线的顶点坐标是它的最高点、且x=
| 5 |
| 2 |
所以当BE的长为
| 5 |
| 2 |
| 5 |
| 4 |

(2)若E在边BC上,CF=y=
| 6 |
| 5 |
| 1 |
| 5 |
∴-
| 1 |
| 5 |
| 6 |
| 5 |
解得x1=2,x2=3,
当BE=2时,tan∠EAF=
| 3 |
| 5 |
当BE=3,时tan∠EAF=
| 2 |
| 5 |
若E在CB延长线上时,同理可得△CEF∽△BAE,
∴
| CF |
| BE |
| CE |
| AB |
| y |
| x |
| 5+x |
| 5 |
∴y=
| 1 |
| 5 |
∵CF=y=
| 6 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
解得:x1=1,x2=-6(舍去),
当BE=1时,tan∠EAF=
| 6 |
| 5 |
当E点可在BC的延长线上,CE=1,
tan∠EAF=
| 1 |
| 5 |
点评:此题综合考查了相似三角形的判定及性质的应用、二次函数的最值求法、直角三角形中锐角函数值的求法等知识点.

练习册系列答案
相关题目
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.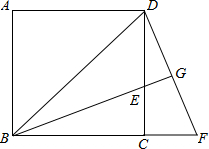 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.