题目内容
1. 如图,AB∥CD,AD平分∠BAC,且∠D=72°,则∠C的度数为( )
如图,AB∥CD,AD平分∠BAC,且∠D=72°,则∠C的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
分析 根据角平分线的定义可得∠BAD=∠CAD,再根据两直线平行,内错角相等可得∠BAD=∠D,从而得到∠CAD=∠D,再利用三角形的内角和定理列式计算即可得解.
解答 解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AB∥CD,
∴∠BAD=∠D=72°,
∴∠CAD=∠D=72°,
在△ACD中,∠C+∠D+∠CAD=180°,
∴72°+∠C+72°=180°,
解得∠C=36°.
故选A
点评 本题考查了平行线的性质,角平分线的定义,三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
13.某区从参加地理学业水平考试的8000名学生中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得到下表;随后汇总整个样本数据,得到部分结果,绘制成如下统计图.
(注:A:优秀(≥90分)、B:良好(≥70分且<90分)、C:及格(≥60分且<70分)、D:不及格(<60分))
表一
请根据图和表所示信息回答下列问题:
(1)样本中,学生地理学成绩平均分为B分,中位数在B内(填等第),众数是
B(填等第).A占的百分比是30%,C占的百分比是15%.
(2)补全条形统计图.
(3)成绩不低于60的为合格,估计这8000名学生的合格人数.

(注:A:优秀(≥90分)、B:良好(≥70分且<90分)、C:及格(≥60分且<70分)、D:不及格(<60分))
表一
| 甲组 | 乙组 | |
| 人数(人) | 120 | 80 |
| 平均分(分) | 88 | 83 |
(1)样本中,学生地理学成绩平均分为B分,中位数在B内(填等第),众数是
B(填等第).A占的百分比是30%,C占的百分比是15%.
(2)补全条形统计图.
(3)成绩不低于60的为合格,估计这8000名学生的合格人数.

10.下列图形中,∠1与∠2互为补角的是( )
| A. |  | B. |  | C. |  | D. |  |
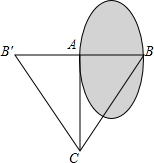 如图,测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,这个测量用到三角形全等判定方法是ASA.
如图,测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,这个测量用到三角形全等判定方法是ASA. 如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈$\frac{12}{13}$,cos72°≈$\frac{5}{13}$,tan72°$≈\frac{12}{5}$)
如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈$\frac{12}{13}$,cos72°≈$\frac{5}{13}$,tan72°$≈\frac{12}{5}$)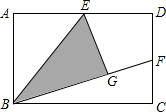 (1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由. 在?ABCD中,延长DA至E,延长BC至F,使AE=CF,连结EF分别交AB和CD于G、H.求证:BG=DH.
在?ABCD中,延长DA至E,延长BC至F,使AE=CF,连结EF分别交AB和CD于G、H.求证:BG=DH.