题目内容
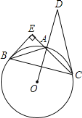
【题目】如图,![]() 内接于
内接于![]() ,过点
,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() ,且
,且![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线.
的切线.
![]() 若
若![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接![]() ,由半径
,由半径![]() 垂直于
垂直于![]() ,利用垂径定理得到
,利用垂径定理得到![]() 为
为![]() 的中点,可得出两条弧相等,根据等弧对等角可得出
的中点,可得出两条弧相等,根据等弧对等角可得出![]() ,又
,又![]() 为圆
为圆![]() 的切线,根据弦切角等于夹弧所对的圆周角可得出
的切线,根据弦切角等于夹弧所对的圆周角可得出![]() ,等量代换可得出三个角相等,由
,等量代换可得出三个角相等,由![]() 与
与![]() 垂直得到
垂直得到![]() 为直角,可得出三个角都为
为直角,可得出三个角都为![]() ,再利用同弧所对的圆心角等于所对圆周角的
,再利用同弧所对的圆心角等于所对圆周角的![]() 倍,可得出
倍,可得出![]() 为
为![]() ,又
,又![]() 为
为![]() ,在三角形
,在三角形![]() 中,利用三角形的内角和定理得到
中,利用三角形的内角和定理得到![]() 为
为![]() ,根据垂直的定义得到
,根据垂直的定义得到![]() 垂直于
垂直于![]() ,即可得出此时
,即可得出此时![]() 为圆
为圆![]() 的切线;
的切线;
(2)由![]() ,且
,且![]() 为
为![]() ,得到三角形
,得到三角形![]() 为等边三角形,根据等边三角形的三边长相等可得出
为等边三角形,根据等边三角形的三边长相等可得出![]() ,由
,由![]() 的长得出
的长得出![]() 的长,在直角三角形
的长,在直角三角形![]() 中,利用锐角三角函数定义表示出
中,利用锐角三角函数定义表示出![]() ,将
,将![]() 及
及![]() 的值代入即可求出
的值代入即可求出![]() 的长.
的长.
![]() 连接
连接![]() ,如图所示:
,如图所示:
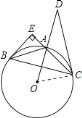
∵![]() ,且
,且![]() 为圆心,
为圆心,
∴点![]() 为
为![]() 的中点,即
的中点,即![]() ,
,
∴![]() ,
,
又![]() 为切线,
为切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
则![]() 为圆
为圆![]() 切线;
切线;
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
则![]() .
.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目