题目内容
6.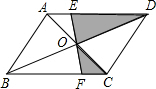 如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )
如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )| A. | 4 | B. | 2 | C. | 6 | D. | 无法确定 |
分析 先根据平行四边形的性质得出OB=OD,∠FBO=∠EDO,再由全等三角形的判定得到△OFB≌△OED,从而将阴影部分的面积转化为规则的几何图形的面积进行计算.
解答 解:∵四边形ABCD是平行四边形,
∴OB=OD,∠FBO=∠EDO.
在△OFB与△OED中
$\left\{\begin{array}{l}{∠FBO=∠EDO}\\{OB=OD}\\{∠FOB=∠EOD}\end{array}\right.$,
∴△FBO≌△EDO,
∴S阴影部分=S△BOC=$\frac{1}{4}$S?ABCD=$\frac{1}{4}$×8=2.
故选B.
点评 本题主要考查了平行四边形的性质以及全等三角形的判定,并通过此题让学生明白求阴影部分的面积一般的思路是将不规则的阴影部分转化为规则的几何图形求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16.已知点(-1,y1),(2,y2)都在直线y=-2x+1上,则y1与y2大小关系是( )
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
17.关于一次函数y=2x-1,下列说法中,正确的是( )
| A. | 图象经过第二象限 | B. | 函数值y随x的增大而减小 | ||
| C. | 图象在x轴上的截距是1 | D. | 图象在y轴上的截距是-1 |
11.计算7-4的结果是( )
| A. | 3 | B. | -3 | C. | 11 | D. | -11 |
18.下列各式中,正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{27}$=-3 | C. | ±$\sqrt{16}$=4 | D. | $\sqrt{(-4)^{3}}$=-4 |
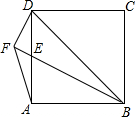 如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.
如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.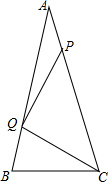 如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.
如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.