题目内容
已知直线y1=x，y2=| 1 |
| 3 |
| 4 |
| 5 |
分析：y始终取三个函数的最小值，y最大值即求三个函数的公共部分的最大值．
解答：
解：如图，分别求出y1，y2，y3交点的坐标A（
，
）；B（
，
）；C（
，
）
当x＜
，y=y1；
当
≤x＜
，y=y2；
当
≤x＜
，y=y2；
当x≥
，y=y3．
∵y总取y1，y2，y3中的最小值，
∴y最大=
．
解：如图，分别求出y1，y2，y3交点的坐标A（| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 9 |
| 25 |
| 9 |
| 60 |
| 17 |
| 37 |
| 17 |
当x＜
| 3 |
| 2 |
当
| 3 |
| 2 |
| 25 |
| 9 |
当
| 25 |
| 9 |
| 60 |
| 17 |
当x≥
| 60 |
| 17 |
∵y总取y1，y2，y3中的最小值，
∴y最大=
| 37 |
| 17 |
点评：此题主要考查了一次函数与一次不等式的综合应用，要先画出函数的图象根据数形结合解题，锻炼了学生数形结合的思想方法．
练习册系列答案
相关题目
过A、B两点，
（2012•贵港）如图，已知直线y1=x+m与y2=kx-1相交于点P（-1，1），则关于x的不等式x+m＞kx-1的解集在数轴上表示正确的是（ ）
如图，已知直线y1=x+m与x轴、y轴分别交于A、B，与双曲线
如图，已知直线y1=k1x+b1分别与x轴，y轴交于点A、B，另一条直线y2=k2x+b2经过点C（0，1），且把△AOB分成面积相等的两部分，试分别确定两条直线的解析式．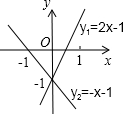
已知直线y1=2x-1和y2=-x-1的图象如图所示，根据图象填空．当x