��Ŀ����
17��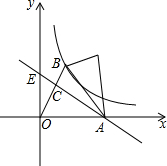 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��AOBΪ�ȱ������Σ���A�������ǣ�4$\sqrt{3}$��0������B�ڵ�һ���ޣ�AC�ǡ�OAB��ƽ���ߣ�������y�ύ�ڵ�E����MΪֱ��AC��һ�����㣬�ѡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���B�غϣ��õ���ABD�����跴��������y=$\frac{k}{x}$��x��0��ͼ����B
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��AOBΪ�ȱ������Σ���A�������ǣ�4$\sqrt{3}$��0������B�ڵ�һ���ޣ�AC�ǡ�OAB��ƽ���ߣ�������y�ύ�ڵ�E����MΪֱ��AC��һ�����㣬�ѡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���B�غϣ��õ���ABD�����跴��������y=$\frac{k}{x}$��x��0��ͼ����B��1����M���E�غ�ʱ������������y=$\frac{k}{x}$��ͼ���Ƿ�AD���е㣿Ϊʲô��
��2���Ƿ���ڵ�M��ʹ����������y=$\frac{k}{x}$��ͼ��ؾ���AD���е㣿�����������M�����꣬����������˵�����ɣ�
���� ��1����M���E�غ�ʱ������������y=$\frac{k}{x}$��ͼ����AD���е㣮���ɣ���AD���е�Ϊ��F����BH��OA���ɡ�AOBΪ�ȱ������Σ���A�������ǣ�4$\sqrt{3}$��0���������OA=OB=4$\sqrt{3}$��OH=HA=$\frac{1}{2}$OA=2$\sqrt{3}$��Ȼ����Rt��BOH�У��ɹ��ɶ�������BH��ֵ������ȷ��B������꣬�ɷ���������y=$\frac{k}{x}$��x��0��ͼ����B���Ӷ�ȷ�������������Ĺ�ϵʽ��y=$\frac{12\sqrt{3}}{x}$��Ȼ����AC�ǡ�OAB��ƽ���ߣ��ɵá�OAE=��BAE=30�㣬��Rt��AOE�У���30������Ե�ֱ�DZߵ���б�ߵ�һ�룬�ɵ�OE=$\frac{1}{2}$AE���ɹ��ɶ����ã�OA2+OE2=AE2������OE=4�������ɵ�AE=8���ɡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���AB�غϣ��õ���ABD��������ת�����ʣ��ɵ�AD=AE=8����DAB=��MAO=30�㣬�����ɵá�AOD=90�㣬�ɵ�F��AD���е㣬�ɵõ�F������Ϊ����4$\sqrt{3}$��4����Ȼ��F�����������ϵʽ����֤��F���ڷ���������y=$\frac{12\sqrt{3}}{x}$��ͼ���ϣ��Ӷ��õ�����M���E�غ�ʱ������������y=$\frac{k}{x}$��ͼ����AD���е㣻
��2�����ڵ�M��ʹ����������y=$\frac{k}{x}$��ͼ��ؾ���AD���е㣮�ɣ�1��֪��OE=4������ȷ��E��0��4����Ȼ����ֱ��AC�Ĺ�ϵʽΪ��y=kx+b����A��4$\sqrt{3}$��0����E��0��4������������ϵʽ���Ӷ��ɵ�ֱ��AC�Ĺ�ϵʽΪ��y=-$\frac{\sqrt{3}}{3}$x+4���ɵ�M��ֱ��AC�ϣ�����M������Ϊ����a��-$\frac{\sqrt{3}}{3}$a+4���������ɵ�MP=-$\frac{\sqrt{3}}{3}$a+4��Ȼ����30������Ե�ֱ�DZߵ���б�ߵ�һ�룬�ɵ�AM=2MP=-$\frac{2\sqrt{3}}{3}a$+8���ɡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���AB�غϣ��õ���ABD��������ת�����ʣ��ɵ�AD=AM=-$\frac{2\sqrt{3}}{3}$a+8����DAB=��MAO=30�㣬�����ɵá�AOD=90�㣬�Ӷ�ȷ��AD���е�����꣬�ɷ���������y=$\frac{k}{x}$��ͼ��ؾ���AD���е㣬��AD���е㣬����y=$\frac{12\sqrt{3}}{x}$���Ӷ�ȷ��M�����꣮
��� �⣺��1����M���E�غ�ʱ������������y=$\frac{k}{x}$��ͼ����AD���е㣮
���ɣ���AD���е�Ϊ��F����BH��OA��
�ߡ�AOBΪ�ȱ������Σ���A�������ǣ�4$\sqrt{3}$��0����
��OA=OB=4$\sqrt{3}$��OH=HA=$\frac{1}{2}$OA=2$\sqrt{3}$����OAB=60�㣬
��Rt��BOH�У��ɹ��ɶ����ã�BH=$\sqrt{O{B}^{2}-O{H}^{2}}$=6��
��B�����������2$\sqrt{3}$��6����
�෴��������y=$\frac{k}{x}$��x��0��ͼ����B��
��k=xy=12$\sqrt{3}$��
�෴���������Ĺ�ϵʽ��y=$\frac{12\sqrt{3}}{x}$��
��AC�ǡ�OAB��ƽ���ߣ�
���OAE=��BAE=30�㣬
��Rt��AOE��
�ߡ�OAE=30�㣬
��OE=$\frac{1}{2}$AE��
�ɹ��ɶ����ã�OA2+OE2=AE2��
����4$\sqrt{3}$��2+OE2=��2OE��2��
��ã�OE=4��
��AE=8��
�ߡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���AB�غϣ��õ���ABD��
��AD=AE=8����DAB=��MAO=30�㣬
���AOD=��OAB+��DAB=90�㣬
�ߵ�F��AD���е㣬
���F����������4$\sqrt{3}$��4����
��x=4$\sqrt{3}$ʱ��y=$\frac{12\sqrt{3}}{4\sqrt{3}}$=3��4��
���F���ڷ���������y=$\frac{12\sqrt{3}}{x}$��ͼ���ϣ�
����M���E�غ�ʱ������������y=$\frac{k}{x}$��ͼ����AD���е㣮
��2�����ڵ�M��ʹ����������y=$\frac{k}{x}$��ͼ��ؾ���AD���е㣮
�ɣ�1��֪��OE=4��
��E��0��4����
��ֱ��AC�Ĺ�ϵʽΪ��y=kx+b��
��A��4$\sqrt{3}$��0����E��0��4������������ϵʽ�ã�
$\left\{\begin{array}{l}{b=4}\\{4\sqrt{3}k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=4}\end{array}\right.$��
��ֱ��AC�Ĺ�ϵʽΪ��y=-$\frac{\sqrt{3}}{3}$x+4��
�ߵ�M��ֱ��AC�ϣ�
����M����������a��-$\frac{\sqrt{3}}{3}$a+4����
��MP=-$\frac{\sqrt{3}}{3}$a+4��
�ߡ�MAO=30�㣬
��AM=2MP=-$\frac{2\sqrt{3}}{3}a$+8��
�ߡ�AOM�Ƶ�A˳ʱ����ת��ʹ��AO���AB�غϣ��õ���ABD��
��AD=AM=-$\frac{2\sqrt{3}}{3}$a+8����DAB=��MAO=30�㣬
���AOD=��OAB+��DAB=90�㣬
��AD���е������Ϊ����4$\sqrt{3}$��-$\frac{\sqrt{3}}{3}$a+4����
�߷���������y=$\frac{k}{x}$��ͼ��ؾ���AD���е㣬
�ཫAD���е�����꣨4$\sqrt{3}$��-$\frac{\sqrt{3}}{3}$a+4��������y=$\frac{12\sqrt{3}}{x}$�ã�
-$\frac{\sqrt{3}}{3}$a+4=$\frac{12\sqrt{3}}{4\sqrt{3}}$��
��ã�a=-$\sqrt{3}$��
��M��-$\sqrt{3}$��5����
�����ڵ�M��-$\sqrt{3}$��5����ʹ����������y=$\frac{12\sqrt{3}}{x}$��ͼ��ؾ���AD���е㣮
���� �����Ƿ������������ۺ��⣬��Ҫ�����ˣ��ô���ϵ�������ϵʽ�����ɶ�������ƽ��ֱ������ϵ��ȷ����������֪ʶ������Ĺؼ��ǣ���ȷͼ�ε���ת���ı�ͼ�εĴ�С����״��

 Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д� ��ͼ���ڡ�O�У���AB���ڡ�O�İ뾶��OC��AB����O�ڵ�C�����AOC���ڣ�������
��ͼ���ڡ�O�У���AB���ڡ�O�İ뾶��OC��AB����O�ڵ�C�����AOC���ڣ�������| A�� | 80�� | B�� | 50�� | C�� | 40�� | D�� | 30�� |
| A�� | 1 | B�� | -27 | C�� | 1��-27 | D�� | ��ȷ�� |
 ��С�׳��������У�������ͼ��ʾ����O��AB�ľ�����18cm��O��CD�ľ�����6cm������CD�ij�����AB���ģ�������
��С�׳��������У�������ͼ��ʾ����O��AB�ľ�����18cm��O��CD�ľ�����6cm������CD�ij�����AB���ģ�������| A�� | 3�� | B�� | $\frac{1}{2}$ | ||
| C�� | $\frac{1}{3}$ | D�� | ��֪AB�ij��ȣ����ж� |
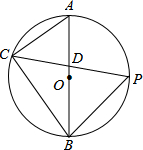 ��ͼ��AB�ǡ�O��ֱ������P��$\widehat{AB}$���е㣮
��ͼ��AB�ǡ�O��ֱ������P��$\widehat{AB}$���е㣮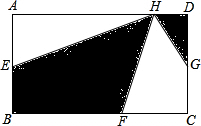 ��ͼ��������ABCD�����Ϊ60ƽ�����ף�AE=EB��BF=FC��CG=GD��HΪAD��������һ�㣬��Ӱ��������ͳ�����ABCD����ı���1��2��
��ͼ��������ABCD�����Ϊ60ƽ�����ף�AE=EB��BF=FC��CG=GD��HΪAD��������һ�㣬��Ӱ��������ͳ�����ABCD����ı���1��2��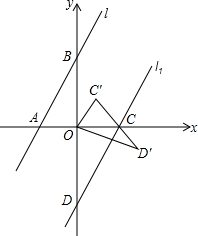 ��ͼ����ֱ֪��l��$y=\sqrt{3}x+3$��x�ᡢy�ύ��A��B���㣬��ֱ��l����ƽ��m����λ���Ⱥ��ֱ��l1��ֱ��l1��x�ᡢy��ֱ���C��D���㣬����COD�Ƶ�O����ʱ�뷽����ת60���õ���C��O��D�䣮����AOB�ա�COD��
��ͼ����ֱ֪��l��$y=\sqrt{3}x+3$��x�ᡢy�ύ��A��B���㣬��ֱ��l����ƽ��m����λ���Ⱥ��ֱ��l1��ֱ��l1��x�ᡢy��ֱ���C��D���㣬����COD�Ƶ�O����ʱ�뷽����ת60���õ���C��O��D�䣮����AOB�ա�COD��