题目内容
函数
与y=x-2的图象的交点坐标为（a，b），求
的值．
解：∵y=
与y=x-2函数交点坐标为（a，b），
∴将x=a，y=b代入y=得：b=
，即ab=3，
代入y=x-2得：b=a-2，即a-b=2，
则=
=
=-
．
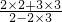分析：由y=与y=x-2函数交点坐标为（a，b），将x=a，y=b代入反比例与一次函数解析式，得到ab及a-b的值，将所求式子变形后，把ab及a-b的值代入即可求出值．
点评：此题考查了反比例函数与一次函数的交点问题，利用了整体代入的思想，根据题意得出ab与a-b的值是解本题的关键．
与y=x-2函数交点坐标为（a，b），∴将x=a，y=b代入y=
得：b=，即ab=3，代入y=x-2得：b=a-2，即a-b=2，
则
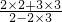===-．分析：由y=
与y=x-2函数交点坐标为（a，b），将x=a，y=b代入反比例与一次函数解析式，得到ab及a-b的值，将所求式子变形后，把ab及a-b的值代入即可求出值．点评：此题考查了反比例函数与一次函数的交点问题，利用了整体代入的思想，根据题意得出ab与a-b的值是解本题的关键．
练习册系列答案
相关题目
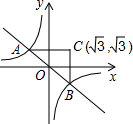如图，反比例函数
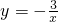与一次函数y=-x的图象交于A、B两点．
），求△ABC的面积．
与一次函数y=-x的图象交于A、B两点．
），求△ABC的面积．
与y=-x2+k的图象的顶点重合，则下列结论不正确的是（ ）
与y=-x2+k的图象的顶点重合，则下列结论不正确的是（ ）