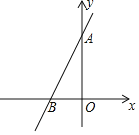题目内容
【题目】已知，如图：直线AB：y＝﹣3x+3与两坐标轴交于A，B两点．
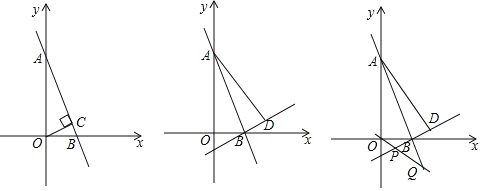
（1）过点O作OC⊥AB于点C，求OC的长；
（2）将△AOB沿AB翻折到△ABD，点O与点D对应，求直线BD的解析式；
（3）在（2）的条件下，正比例函数y＝kx与直线BD交于P，直线AB交于Q，若OP＝3OQ，求正比例函数的解析式．
【答案】（1）
；（2）y＝3x﹣3；（3）
【解析】
（1）首先求出A、B两点的坐标得出OA＝3，OB＝1，据此利用勾股定理求出AB的长，最后通过三角形等面积法进一步求解即可；
（2）连接OD，过点D作DH⊥x轴于H，根据题意证明△AOB~△OHD，然后利用相似三角形性质求出D点坐标，最后利用待定系数法求解析式即可；
（3）过点P作PM⊥x轴于M，点Q作QN⊥x轴于N，根据题意求得OM＝
，ON＝
，结合OP＝3OQ进一步分析求出k＝
，据此即可得出相应的解析式.
（1）∵直线AB解析式为y＝﹣3x+3，
∴A（0，3），B（1，0），
∴OA＝3，OB＝1，
∴AB＝
，
∵△AOB的面积＝
OA×OB＝AB×OC，
∴OC＝
；
（2）连接OD，过点D作DH⊥x轴于H，
∵点O与点D关于AB对称，
∴AB垂直平分OD，由（1）OC＝
，
∴OD＝2OC＝
，
易得：△AOB~△OCB，△OCB~△OHD，
∴△AOB~△OHD，
∴
，
∴DH＝
，OH＝
，
∴D（，）．
设直线BD解析式为y＝kx+b，
∵B（1，0），D（，），
∴
，且
，
解得：
，
，
∴直线BD解析式为y＝3x﹣3．
（3）如图，过点P作PM⊥x轴于M，点Q作QN⊥x轴于N．
∵正比例函数y＝kx与直线BD交于P，
∴kx＝3x﹣3，解得x＝，
∴OM＝，
∵正比例函数y＝kx与直线AB交于Q，
∴kx＝﹣3x+3，解得x＝
∴ON＝，
∵OP＝3OQ，
∴ON＝3OM，
∴＝3×，解得k＝，
∴正比例函数的解析式为．
