题目内容
2.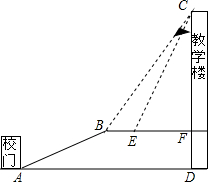 重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米
重庆是一座美丽的山城,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在斜坡B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米(1)求斜坡AB的坡度i;
(2)求教学楼CF的高度.
(参考数据:tan53°≈$\frac{4}{3}$,tan63.4°≈2)
分析 (1)过B作BG⊥AD于G,则四边形BGDF是矩形,求得BG=DF=5,解出AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=12,于是得到AB的坡度i=$\frac{BG}{AG}=\frac{5}{12}$=1:2.4;
(2)在Rt△BCF中,BF=$\frac{CF}{tan∠CBF}$=$\frac{CF}{\frac{4}{3}}$,在Rt△CEF中,EF=$\frac{CF}{tan∠CEF}$=$\frac{CF}{2}$,得到方程BF-EF=$\frac{CF}{\frac{4}{3}}$-$\frac{CF}{2}$=4,解得CF=16即可.
解答 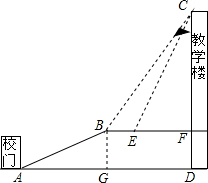 解:(1)过B作BG⊥AD于G,
解:(1)过B作BG⊥AD于G,
则四边形BGDF是矩形,
∴BG=DF=5,
∵AB=13,
∴AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=12,
∴AB的坡度i=$\frac{BG}{AG}=\frac{5}{12}$=1:2.4;
(2)在Rt△BCF中,BF=$\frac{CF}{tan∠CBF}$=$\frac{CF}{\frac{4}{3}}$,
在Rt△CEF中,EF=$\frac{CF}{tan∠CEF}$=$\frac{CF}{2}$,
∵BE=4,
∴BF-EF=$\frac{CF}{\frac{4}{3}}$-$\frac{CF}{2}$=4,
解得:CF=16.
∴教学楼CF的高度=16.
点评 本题考查了解直角三角形的应用-仰角和俯角问题,解直角三角形的应用-坡度和坡比问题,正确理解题意是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
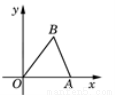
 如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是90°.
如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是90°.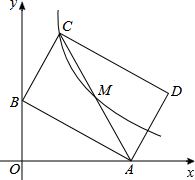 如图,已知:直线y=-$\frac{1}{3}$x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=$\frac{k}{x}$(x>0)正好经过C,M两点,则k=4.
如图,已知:直线y=-$\frac{1}{3}$x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=$\frac{k}{x}$(x>0)正好经过C,M两点,则k=4.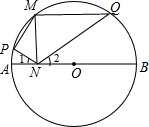 如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤.
如图,AB是⊙O的直径,M是⊙O上一点,MN⊥AB,垂足为N.P,Q分别为弧AM,弧BM上一点(不与端点重合),如果∠MNP=∠MNQ.有以下结论:①∠1=∠2,②∠MPN+∠MQN=180°,③∠MQN=∠PMN,④PM=QM,⑤MN2=PN•QN.其中正确的是①③⑤.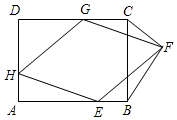 已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.
已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF. 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为a,tana=$\frac{3}{2}$,则t的值是2.
如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为a,tana=$\frac{3}{2}$,则t的值是2.