题目内容
在△AOB的内部有一点P,点P与P1关于OA对称,点P与P2关于BO对称,则△OP1P2是
- A.等边三角形
- B.等腰三角形
- C.直角三角形
- D.钝角三角形
B
分析:根据轴对称的性质可知.
解答:在△AOB的内部有一点P,点P与P1关于OA对称,有PO=P1O,
点P与P2关于BO对称,有PO=P2O,
则△OP1P2是等腰三角形.
故选B.
点评:本题考查轴对称的性质.对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
分析:根据轴对称的性质可知.
解答:在△AOB的内部有一点P,点P与P1关于OA对称,有PO=P1O,
点P与P2关于BO对称,有PO=P2O,
则△OP1P2是等腰三角形.
故选B.
点评:本题考查轴对称的性质.对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
 E呢?若引十条射线一共会有多少个角?
E呢?若引十条射线一共会有多少个角?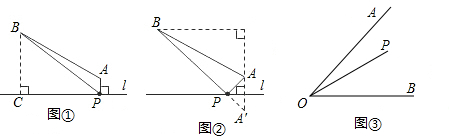
 如图,有两条国道相交于O点,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法).
如图,有两条国道相交于O点,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法).
 CB,点D是直线AB上一点,满足BD=
CB,点D是直线AB上一点,满足BD=