题目内容
4.二次函数y=(x+1)2-5,当m≤x≤n,且mn<0,y的最小值是2m,最大值是2n,则m+n=-$\frac{1}{2}$.分析 由条件m≤x≤n和mn<0可得m<0,n>0所以y的最小值2m为负数,最大值2n为正数.最小值为2m分两种情况:①-1<m<0时,x=m时取得最小值2m;②m≤-1时,函数在x=-1时取得最小值-5,据此分别求解可得.
解答 解:∵mn<0,且m≤x≤n,
∴m<0、n>0,
①当-1<m<0时,x=m时取得最小值2m,x=n时,取得最大值2n,
即$\left\{\begin{array}{l}{(m+1)^{2}-5=2m}&{①}\\{(n+1)^{2}-5=2n}&{②}\end{array}\right.$,
解方程①得:m=2或m=-2(均不符合题意),舍去;
②当m≤-1时,函数在x=-1时取得最小值-5,x=n时取得最大值2n,
即$\left\{\begin{array}{l}{2m=-5}\\{(n+1)^{2}-5=2n}\end{array}\right.$,
解得:m=-$\frac{5}{2}$,n=2或n=-2(舍去),
则m+n=-$\frac{5}{2}$+2=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$
点评 本题考查了二次函数的最值问题,根据二次函数的图象分类讨论是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14.下列实数中,为无理数的是( )
| A. | 3.14 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |

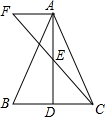 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F.
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F.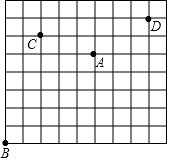 某水库的景区示意图如图所示(网格中每个小正方形的边长为1).若景点A的坐标为(3,3),请在图中画出相应的平面直角坐标系,并写出景点B、C、D的坐标.
某水库的景区示意图如图所示(网格中每个小正方形的边长为1).若景点A的坐标为(3,3),请在图中画出相应的平面直角坐标系,并写出景点B、C、D的坐标.