题目内容
2.一个不透明的袋子中有除颜色外其余都相同的红、黄、蓝色玻璃球若干个,其中红色玻璃球有6个,黄色玻璃球有9个,已知从袋子中随机摸出一个球为蓝色玻璃球的概率为$\frac{3}{8}$,那么,随机摸出一个为红色玻璃球的概率为$\frac{1}{4}$.分析 首先设袋子中篮球x个,由概率公式即可求得方程:$\frac{x}{x+6+9}$=$\frac{3}{8}$,继而求得篮球的个数,然后利用概率公式求解即可求得答案.
解答 解:设袋子中篮球x个,
根据题意得:$\frac{x}{x+6+9}$=$\frac{3}{8}$,
解得:x=9,
经检验:x=9是原分式方程的解;
∴随机摸出一个为红色玻璃球的概率为:$\frac{6}{9+6+9}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
7.在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
7.若关于x的分式方程$\frac{m-1}{x-1}$=2的解不大于2,则m的取值范围是( )
| A. | m≤3 | B. | m≠1 | C. | m<3且m≠-1 | D. | m≤3且m≠1 |
14. 几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
 几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )
几个棱长为1的正方体组成几何体的三视图如图,则这个几何体的体积是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |




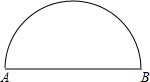 小军在为班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助他设计一个合理的等分方案.(要求:不写作法,保留作图痕迹,写出结论.)
小军在为班级办黑板报时遇到了一个难题,在版面设计过程中需将一个半圆面三等分,请你帮助他设计一个合理的等分方案.(要求:不写作法,保留作图痕迹,写出结论.)