题目内容
 已知关于x的一元二次方程x2-mx+m-1=0.
已知关于x的一元二次方程x2-mx+m-1=0.(1)求证:无论m取任何实数时,方程总有实数根;
(2)关于x的二次函数y1=x2-mx+m-1的图象C1经过(k-1,k2-6k+8)和(-k+5,k2-6k+8)两点.
①求这个二次函数的解析式;
②把①中的抛物线C1沿x轴翻折后,再向左平移2个单位,向上平移8个单位得到抛物线C2.设抛物线C2交x轴于M、N两点(点M在点N的左侧),点P(a,b)为抛物线C2在x轴上方部分图象上的一个动点.当∠MPN≤45°时,直接写出a的取值范围.
考点:二次函数综合题
专题:
分析:(1)通过一元二次方程根的判别式即可证明.
(2)①根据x=
和x=-
即可求得m的值,进而求得解析式.
②作出△MNP的外接圆,找出圆心为(0,3),然后根据勾股定理即可求得.
(2)①根据x=
| x1+x2 |
| 2 |
| b |
| 2a |
②作出△MNP的外接圆,找出圆心为(0,3),然后根据勾股定理即可求得.
解答:(1)证明:在x2-mx+m-1=0中,△=m2-4(m-1)=m2-4m+4=(m-2)2
∵当m取任何值时,(m-2)2≥0,
∴无论m取任何实数时,方程总有实数根.
(2)解:①∵抛物线y1=x2-mx+m-1过点(k-1,k2-6k+8)和点(-k+5,k2-6k+8).
∴抛物线y1=x2-mx+m-1,
∵对称轴为:x=
=2,
∴x=
=2,解得m=4.
∴y1=x2-4x+3
②如图所示:-
≤a≤
;
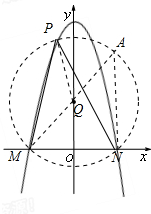
∵y1=x2-4x+3=(x-2)-12,
∴抛物线C1沿x轴翻折后,再向左平移2个单位,向上平移8个单位得到抛物线C2为y2=-x2+9,
∴M(-3,0),N(3,0),
作出△MNP的外接圆,过N点作AN⊥x轴,交圆于A,连接AM交y轴于Q点,Q既是圆心,
∵∠A=∠MPN=45°
∴∠OMQ=45°,
∴Q(0,3),
∴PQ=MQ=3
,
∵P(a,-a2+9),
∴PQ2=a2+(-a2+9-3)2=(3
)2
即a4-11a2+18=0,解得a=
或a=-
,或a=3(舍去),a=-3(舍去),
故-
≤a≤
;
∵当m取任何值时,(m-2)2≥0,
∴无论m取任何实数时,方程总有实数根.
(2)解:①∵抛物线y1=x2-mx+m-1过点(k-1,k2-6k+8)和点(-k+5,k2-6k+8).
∴抛物线y1=x2-mx+m-1,
∵对称轴为:x=
| (k-1)+(-k+5) |
| 2 |
∴x=
| m |
| 2 |
∴y1=x2-4x+3
②如图所示:-
| 2 |
| 2 |

∵y1=x2-4x+3=(x-2)-12,
∴抛物线C1沿x轴翻折后,再向左平移2个单位,向上平移8个单位得到抛物线C2为y2=-x2+9,
∴M(-3,0),N(3,0),
作出△MNP的外接圆,过N点作AN⊥x轴,交圆于A,连接AM交y轴于Q点,Q既是圆心,
∵∠A=∠MPN=45°
∴∠OMQ=45°,
∴Q(0,3),
∴PQ=MQ=3
| 2 |
∵P(a,-a2+9),
∴PQ2=a2+(-a2+9-3)2=(3
| 2 |
即a4-11a2+18=0,解得a=
| 2 |
| 2 |
故-
| 2 |
| 2 |
点评:本题考查了二次方程的根的判别式以及抛物线的顶点坐标的求法,构建等腰直角三角形是本题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
小明家承包的果园,前年水果产量为50吨,后来改进了种植技术,今年的总产量是60.5吨,小明家去年,今年平均每年的粮食产量增长率是( )
| A、5% | B、10% |
| C、15% | D、20% |
 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
 如图,是4×4正方形网格,请在其中选取一白色的小正方形并涂黑,使图中黑色部分形成一个中心对称图形,并在图中用O点标出对称中心.
如图,是4×4正方形网格,请在其中选取一白色的小正方形并涂黑,使图中黑色部分形成一个中心对称图形,并在图中用O点标出对称中心. 如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么?
如图,六边形ABCDEF的内角都相等,∠DAB=60°.AB与DE有什么关系?为什么? 七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
七(1)班同学为了解2013年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.