题目内容
9.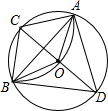 如图,CD为⊙O直径,以C点为圆心,CO为半径作弧,交⊙O于A、B两点,求证:AD=BD=BA.
如图,CD为⊙O直径,以C点为圆心,CO为半径作弧,交⊙O于A、B两点,求证:AD=BD=BA.
分析 利用CA=CB=CO可判断△OBC和△OAC都是等边三角形,则∠BCO=∠ACO=60°,∠BOC=∠AOC=60°,根据圆周角定理得∠ADB=60°,即∠ACD=∠BCD=∠ADB,所以$\widehat{AD}$=$\widehat{BD}$=$\widehat{AB}$,然后根据圆心角、弧、弦的关系易得AD=BD=BA.
解答 证明:∵CA=CB=CO,
∴OB=BC=OC=OA=AC,
∴△OBC和△OAC都是等边三角形,
∴∠BCO=∠ACO=60°,∠BOC=∠AOC=60°,
∴∠AOB=120°,
∴∠ADB=60°,
∴∠ACD=∠BCD=∠ADB,
∴$\widehat{AD}$=$\widehat{BD}$=$\widehat{AB}$,
∴AD=BD=BA.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边三角形的判定与性质.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由.
如图,点D,E分别是ABC的边BC,AC上的点,BE,AD交于F,已知AB=AC,∠BAC=∠AFE=2∠ACB=2α,G为AC上的点,∠AEB=∠CGD.探究线段AE,GC的数量关系,并说明理由. 如图,∠AOB=90°,∠AOD=160°,OC平分∠BOD,求∠COD及∠AOC的度数.
如图,∠AOB=90°,∠AOD=160°,OC平分∠BOD,求∠COD及∠AOC的度数.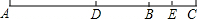 如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点.
如图,已知线段AB,延长AB到点C,使BC=$\frac{1}{4}$AB,点D为AC的中点,点E是BC的中点.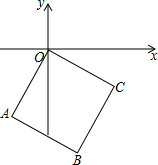 已知边长为6的正方形OABC在直角坐标系中,(如图)OA与y轴的夹角为30°.求点A、点B、点C的坐标.
已知边长为6的正方形OABC在直角坐标系中,(如图)OA与y轴的夹角为30°.求点A、点B、点C的坐标.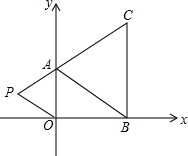 如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.
如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.