题目内容
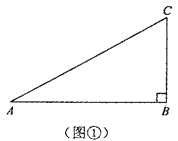
【题目】如图,矩形ABCD中,AB=![]() ,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.
,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.

【答案】1、![]() 、2﹣
、2﹣![]()
【解析】
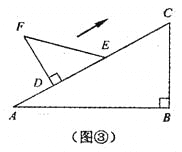
过点C作CM⊥DF,垂足为点M,判断△CDF是等腰三角形,要分类讨论,①CF=CD;②DF=DC;③FD=FC,根据相似三角形的性质进行求解.
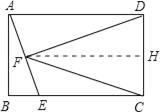
①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,
延长CM交AD于点G,
∴AG=GD=1,
∴CE=1,
∵CG∥AE,AD∥BC,
∴四边形AGCE是平行四边形,
∴CE=AG=1,
∴BE=1
∴当BE=1时,△CDF是等腰三角形;
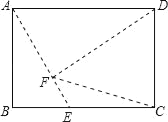
②DF=DC时,则DC=DF=![]() ,
,
∵DF⊥AE,AD=2,
∴∠DAE=45°,
则BE=![]() ,
,
∴当BE=![]() 时,△CDF是等腰三角形;
时,△CDF是等腰三角形;
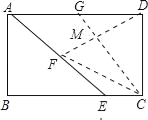
③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB=![]() ,BE=x,
,BE=x,
∴AE=![]() ,
,
AF=![]() ,
,
∵△ADF∽△EAB,
∴![]() ,
,
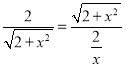 ,
,
x2﹣4x+2=0,
解得:x=2±![]() ,
,
∴当BE=2﹣![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
综上,当BE=1、![]() 、2﹣
、2﹣![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
故答案为:1、![]() 、2﹣
、2﹣![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
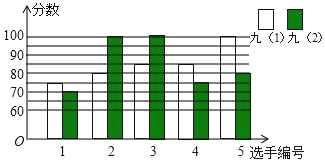
【题目】为选拔优秀选手参加瑶海区第八届德育文化艺术节“诵经典”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示
(1)根据图示填写下表
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 |
| 85 |
九(2) |
| 80 |
|
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班五名选手的成绩较稳定.