题目内容
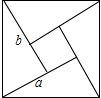 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积分别是为1、13,则直角三角形两直角边和a+b=
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积分别是为1、13,则直角三角形两直角边和a+b=考点:勾股定理的证明
专题:
分析:根据大正方形的面积即可求得c2,利用勾股定理可以得到a2+b2=c2,然后求得直角三角形的面积即可求得ab的值,根据(a+b)2=a2+b2+2ab=c2+2ab即可求解.
解答:解:∵大正方形的面积是13,
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是
=3,
又∵直角三角形的面积是
ab=3,
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25.
∴a+b=5(舍去负值).
故答案是:5.
∴c2=13,
∴a2+b2=c2=13,
∵直角三角形的面积是
| 13-1 |
| 4 |
又∵直角三角形的面积是
| 1 |
| 2 |
∴ab=6,
∴(a+b)2=a2+b2+2ab=c2+2ab=13+2×6=13+12=25.
∴a+b=5(舍去负值).
故答案是:5.
点评:本题考查了勾股定理以及完全平方公式.注意完全平方公式的展开:(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.

练习册系列答案
相关题目
如果两个有理数的和是负数,那么这两个数一定是( )
| A、绝对值不相等 |
| B、都是负数 |
| C、一正一负 |
| D、至少一个负数 |
 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE,若AB=
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE,若AB= 画出如图所示几何体的主视图、左视图、俯视图.
画出如图所示几何体的主视图、左视图、俯视图. 如图,在长为32m,宽为20m的长方形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.
如图,在长为32m,宽为20m的长方形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.