题目内容
 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE,若AB=
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC、CE,若AB=| 34 |
考点:圆周角定理,等腰三角形的性质,勾股定理
专题:
分析:根据圆周角定理由AB是⊙O的直径得到∠ACB=90°,而DC=CB,根据线段的垂直平分线的判定与性质得AB=AD,于是得到∠B=∠D;然后设AC=x,则BC=x+2,在Rt△ABC中,利用勾股定理可计算出解得x=3或-5(舍去),即BC=5,由于∠E=∠B,则∠D=∠E,所以CE=5.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°,
又∵DC=CB,
∴AC垂直平分DB,
∴AB=AD,
∴∠B=∠D;
设AC=x,则BC=x+2,
在Rt△ABC中,(x+2)2+x2=(
)2,
解得x=3或-5(舍去),即BC=5,
∵∠E=∠B,
∴∠D=∠E,
∴CE=CD=BC=5.
故答案为:5.
∴∠ACB=90°,
又∵DC=CB,
∴AC垂直平分DB,
∴AB=AD,
∴∠B=∠D;
设AC=x,则BC=x+2,
在Rt△ABC中,(x+2)2+x2=(
| 34 |
解得x=3或-5(舍去),即BC=5,
∵∠E=∠B,
∴∠D=∠E,
∴CE=CD=BC=5.
故答案为:5.
点评:此题考查了圆周角定理、线段垂直平分线的性质、等腰三角形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
下列命题的逆命题不正确的是( )
| A、直角三角形中斜边上的中线等于斜边的一半 |
| B、两直线平行,内错角相等 |
| C、等腰三角形的两个底角相等 |
| D、对顶角相等 |
下列单项式中,次数为5的是( )
| A、3x5y2 |
| B、-2x3y2 |
| C、-22x2y |
| D、4x5y |
下列代数式中,是单项式的有几个( )
x+1;
;πr2 -
a2b;
.
x+1;
| 1 |
| x |
| 2 |
| 3 |
| a+b |
| 2 |
| A、1个 | B、2个 | C、4个 | D、没有 |
下列说法正确的是( )
| A、两点之间直线最短 |
| B、画出AB两点间的距离 |
| C、连接点A与点B的线段,叫做AB两点间的距离 |
| D、两点之间的距离是一个数,不是指线段本身 |
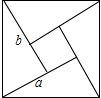 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积分别是为1、13,则直角三角形两直角边和a+b=
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积分别是为1、13,则直角三角形两直角边和a+b=