题目内容
 EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则AH:AE=________.
EFGH是矩形ABCD的内接矩形,且EF:FG=3:1,AB:BC=2:1,则AH:AE=________.
5:1
分析:设AH=a,AE=b,首先证明△AHE≌△CFG,然后证明△CGF∽△BFE,进而得出 =
= =
= =3,再据AB:BC=2:1,即可得a、b的比.
=3,再据AB:BC=2:1,即可得a、b的比.
解答:设AH=a,AE=b,
∵∠CFG=∠DGH=∠AHE=∠FEB,∠HAE=∠FCG=90°,AE=CG,
∴△AHE≌△CFG(AAS);
由三角分别相等可判定△CGF∽△BFE,
∴ =
= =
= =3,即EB=3a,BF=3b,
=3,即EB=3a,BF=3b,
∵AB:BC=2:1,
∴ =2,即a=5b,故AH:AE=5:1.
=2,即a=5b,故AH:AE=5:1.
点评:本题主要考查相似三角形相似的判定及性质、全等的判定和性质、矩形的性质等知识点,找到相应线段的关系比是解题的关键.
分析:设AH=a,AE=b,首先证明△AHE≌△CFG,然后证明△CGF∽△BFE,进而得出
 =
= =
= =3,再据AB:BC=2:1,即可得a、b的比.
=3,再据AB:BC=2:1,即可得a、b的比.解答:设AH=a,AE=b,
∵∠CFG=∠DGH=∠AHE=∠FEB,∠HAE=∠FCG=90°,AE=CG,
∴△AHE≌△CFG(AAS);

由三角分别相等可判定△CGF∽△BFE,
∴
 =
= =
= =3,即EB=3a,BF=3b,
=3,即EB=3a,BF=3b,∵AB:BC=2:1,
∴
 =2,即a=5b,故AH:AE=5:1.
=2,即a=5b,故AH:AE=5:1.点评:本题主要考查相似三角形相似的判定及性质、全等的判定和性质、矩形的性质等知识点,找到相应线段的关系比是解题的关键.

练习册系列答案
相关题目
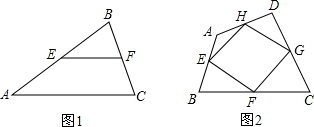
 已知:如图:AD⊥BC于D,点E是边AB上一动点,四边形EFGH是矩形,其中点F,G在BC上,点H在AC上.
已知:如图:AD⊥BC于D,点E是边AB上一动点,四边形EFGH是矩形,其中点F,G在BC上,点H在AC上.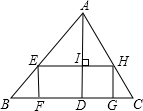 如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积.
如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积. 如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积.
如图所示,四边形EFGH是三角形ABC的内接矩形,AD⊥BC,垂足为D,BC=21cm,AD=14cm,EF:FG=1:2,求矩形EFGH的面积.