题目内容
7.如果$\frac{a}{b}=\frac{3}{5}$,那么$\frac{2a-b}{b}$=$\frac{1}{5}$.分析 利用已知得出a=$\frac{3}{5}$b,进而代入代数式求出答案.
解答 解:∵$\frac{a}{b}=\frac{3}{5}$,
∴a=$\frac{3}{5}$b,
∴$\frac{2a-b}{b}$=$\frac{\frac{6}{5}b-b}{b}$=$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 此题主要考查了比例的性质,正确得出a=$\frac{3}{5}$b是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.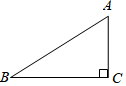 如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )
 如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$. |
2.若(a-b)•(a-b)3•(a-b)m=(a-b)11,则m的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
17.因为cos60°=$\frac{1}{2}$,cos240°=-$\frac{1}{2}$,所以cos240°=cos(180°+60°)=-cos60°;由此猜想、推理知:当α为锐角时有cos(180°+α)=-cosα,由此可知:cos210°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\sqrt{3}$ |
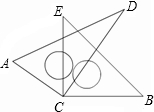 如图,将两块直角三角尺的直角顶点C叠放在一起.
如图,将两块直角三角尺的直角顶点C叠放在一起.