题目内容
运用分解因式法解下列方程:
(1)(x-2)2-2(x-2)=0;
(2)25x2-4=0;
(3)(x-2)2-9=0;
(4)x2+2x-8=0.
(1)(x-2)2-2(x-2)=0;
(2)25x2-4=0;
(3)(x-2)2-9=0;
(4)x2+2x-8=0.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法
专题:计算题
分析:(1)方程左边提取公因式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(2)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(4)方程左边利用十字相乘法分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
(2)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(3)方程左边利用平方差公式分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解;
(4)方程左边利用十字相乘法分解后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答:解:(1)分解因式得:(x-2)(x-2-2)=0,
可得x-2=0或x-4=0,
解得:x1=2,x2=4;
(2)方程分解因式得:(5x+2)(5x-2)=0,
可得5x+2=0或5x-2=0,
解得:x1=-
,x2=
;
(3)分解因式得:(x-2+3)(x-2-3)=0,
可得x+1=0或x-5=0,
解得:x1=-1,x2=5;
(4)分解因式得:(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x1=2,x2=-4.
可得x-2=0或x-4=0,
解得:x1=2,x2=4;
(2)方程分解因式得:(5x+2)(5x-2)=0,
可得5x+2=0或5x-2=0,
解得:x1=-
| 2 |
| 5 |
| 2 |
| 5 |
(3)分解因式得:(x-2+3)(x-2-3)=0,
可得x+1=0或x-5=0,
解得:x1=-1,x2=5;
(4)分解因式得:(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x1=2,x2=-4.
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
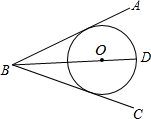 已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切.
已知O是∠ABC的角平分线BD上的一点,以点O为圆心的⊙O与AB相切,求证:BC与⊙O相切.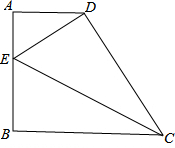 在直角梯形ABCD中,∠A=∠B=90°,AD=3,BC=6,AB=m(m>3),ED⊥CD且交AB于点E,
在直角梯形ABCD中,∠A=∠B=90°,AD=3,BC=6,AB=m(m>3),ED⊥CD且交AB于点E, 如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.
如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).