题目内容
先因式分解(1),(2),(3),再解答后面的问题.
(1)1+a+a(1+a).
(2)1+a+a(1+a)+a(1+a)2.
(3)1+a+a(1+a)+a(1+a)2+a(1+a)3.
问题
:
①先探索上述因式分解的规律,然后写出1+a+a(1+
a)+a(1+a)2+a(1+a)3+…+a(1+a)2014因式分解的结果.
②请按上述方法因式分解:1+a+a(1+a)+a(1+a)2+a(1+a)3+…+a(1+a)n(n为正整数).
【解析】(1)原式=(1+a)(1+a)=(1+a)2.
(2)原式=(1+a)[1+a+a(1+a)]=(1+a)(1+a)(1+a)=(1+a)3.
(3)原式=(1+a)[1+a+a(1+a)+a(1+a)2]
=(1+a)(1+a)[1+a+a(1+a)]
=(1+a)2(1+a)(1+a)
=(1+a)4.
①由(1),(2),(3)的规律可知,1+a+a(1+a)+a(1+a)2+a(1+a)3+…+a(1+a)2014=(1+a)2015.
②原式=(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-1]
=(1+a)(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-2]
=(1+a)2(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-3]
…
=(1+a)n-1(1+a)(1+a)=(1+a)n+1.
练习册系列答案
阅读快车系列答案
相关题目
间却留有一个小正方形,你能利用它们之间的面积关系,得到关于a,b,c的等式吗?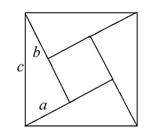
的二次三项式x2+mx+n有一个因式(x+5),且m+n=17,试求m,n的值.
PM⊥AC于点M，求证：BN=CM．