题目内容
18.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1、x2,则有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,则已知一个直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根,则这个直角三角形的斜边长是$\sqrt{11}$.分析 设直角三角形的两条直角边的长分别为m、n,根据根与系数的关系可得出m+n=4、mn=$\frac{7}{2}$,根据勾股定理即可得出斜边$\sqrt{{m}^{2}+{n}^{2}}$的长度,此题得解.
解答 解:设直角三角形的两条直角边的长分别为m、n,
∴m+n=4,mn=$\frac{7}{2}$,
∴$\sqrt{{m}^{2}+{n}^{2}}$=$\sqrt{(m+n)^{2}-2mn}$=$\sqrt{11}$.
故答案为:$\sqrt{11}$.
点评 本题考查了根与系数的关系以及勾股定理,根据根与系数的关系得出m+n=4、mn=$\frac{7}{2}$是解题的关键.

练习册系列答案
相关题目
13.在实数π,-$\frac{2}{5}$,0,-3.14,6.1010010001…中无理数有( )
| A. | 1 个 | B. | 2个 | C. | 3个 | D. | 4个 |
8. 若有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )
若有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )
 若有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )
若有理数a、b在数轴上对应的位置如图所示,则下列关系正确的是( )| A. | |a|<|b| | B. | a>b | C. | a<b | D. | a=b |
 如图,∠BAC=90°,AB=AC,CE⊥AD于E,BF⊥AD于F,若AF=8cm,EF=5cm,则BF=13,CE=8.
如图,∠BAC=90°,AB=AC,CE⊥AD于E,BF⊥AD于F,若AF=8cm,EF=5cm,则BF=13,CE=8.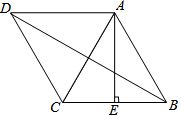 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为1:$\sqrt{3}$..
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为1:$\sqrt{3}$..