题目内容
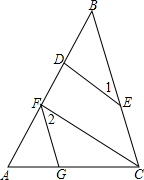在△ABC中，CF⊥AB于点F，ED⊥AB于点D，∠1=∠2，求证：△AFG∽△ABC．考点：相似三角形的判定
专题：证明题
分析：由条件可证得∠AFG=∠B，结合公共角，可证得结论．
解答：证明：∵CF⊥AB，ED⊥AB，
∴∠EDB=∠CFA=90°，
∴∠1+∠B=∠2+∠AFG=90°，且∠1=∠2，
∴∠AFG=∠B，且∠FAG=∠GAC，
∴△AFG∽△ABC．
∴∠EDB=∠CFA=90°，
∴∠1+∠B=∠2+∠AFG=90°，且∠1=∠2，
∴∠AFG=∠B，且∠FAG=∠GAC，
∴△AFG∽△ABC．
点评：本题主要考查相似三角形的判定，掌握相似三角形的判定方法是解题的关键，即有两角对应相等的两个三角形相似．
练习册系列答案
相关题目
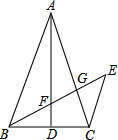如图，已知△ABC中，AB=AC，D为BC的中点，CE∥AB，BE交AD、AC于E、G，求证：BF2=FG•FE．
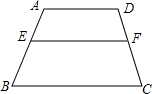如图，在梯形ABCD中，AD∥BC，EF∥BC，若AD=12cm，BC=17cm，AE：EB=2：3，则EF=
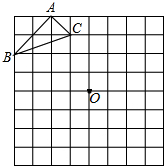在如图所示的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点），按要求画出下列图形（不写画法，保留作图痕迹）．
如图，△ABC中，∠ACB=90°，D是AB的中点，DE⊥AB交AC于E，BC=6cm，sin∠A=