题目内容
2.男女运动员各一名在环形跑道上练习长跑,男运动员比女运动员速度快,他们从同一起点沿相反方向同时出发,每隔25秒相遇一次.现在他们从同一起跑点沿相同方向同时出发,经过25分钟男运动员追上女运动员,并且比女运动员多跑20圈.求:(1)男运动员的速度是女运动员的多少倍?
(2)男运动员追上女运动员时,女运动员跑了多少圈?
分析 (1)由“他们从同一起点沿相反方向同时出发,每隔25秒钟相遇一次”得到等量关系:男运动员所跑路程+女运动员所跑路程=环形跑道的周长;由“他们从同一起跑点沿相同方向同时出发,经过25分钟男运动员追上女运动员,并且比女运动员多跑20圈”,知经过$\frac{25}{20}$分钟男运动员追上女运动员,并且比女运动员多跑了1圈,得到等量关系:男运动员所跑路程-女运动员所跑路程=环形跑道的周长,据此列出方程组,求出问题的解.
(2)由(1)中求出的男运动员的速度与女运动员的速度的比为2:1,可知在时间相同时,他们所行的路程比也为2:1.如果设女运动员跑了x圈,那么男运动员跑了2x圈.根据男运动员比女运动员多跑了20圈列式解答即可.
解答 解:(1)设男运动员的速度是v1米/秒,女运动员的速度是v2米/秒.环形跑道的周长为s米.
由题意得,$\left\{\begin{array}{l}{25({v}_{1}+{v}_{2})=s}\\{25×\frac{60}{20}({v}_{1}-{v}_{2})=s}\end{array}\right.$,
整理得,4v2=2v1,
即v1=2v2.
答:男运动员速度是女运动员速度的2倍;
(2)设女运动员跑了x圈,那么男运动员跑了2x圈.
根据题意,得2x-x=20,
解得,x=20.
故经过了25分钟女运动员跑了20圈.
点评 本题考查分式方程、一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.本题要注意追及问题和相遇问题不同的求解方法及时间相同,路程比等于速度比.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
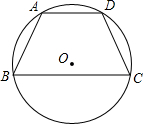 如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.
如图,四边形ABCD内接于⊙O,AD∥BC,求证:AB=CD.
 如图,在四边形ABCD中,∠A=54°,∠B=104°,∠C=76°,则∠D=126度.
如图,在四边形ABCD中,∠A=54°,∠B=104°,∠C=76°,则∠D=126度.