题目内容
 如图,
如图, 是半径为1的圆弧,△AOC为等边三角形,D是
是半径为1的圆弧,△AOC为等边三角形,D是 上的一动点,则四边形AODC的面积s的取值范围是
上的一动点,则四边形AODC的面积s的取值范围是
- A.
 ≤s≤
≤s≤
- B.
 <s≤
<s≤
- C.
 ≤s≤
≤s≤
- D.
 <s<
<s<
B
分析:根据题意,得四边形AODC的最小面积即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD= ,得其面积是
,得其面积是 ;要求最大面积,只需再进一步求得三角形DOC的面积,即是
;要求最大面积,只需再进一步求得三角形DOC的面积,即是 ,则最大面积是
,则最大面积是 .
.
解答: 解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
作CH⊥AO于H,
∵△AOC为等边三角形
∴CH=
∴S△AOC= ;
;
当OD⊥OC时面积最大,
∴S△OCD= ,则最大面积是
,则最大面积是 +
+ =
=
∴四边形AODC的面积s的取值范围是 <s≤
<s≤ .
.
故选B.
点评:此题首先要能够正确分析出要求的四边形的最小面积和最大面积,然后根据等边三角形的性质以及三角形的面积公式进行计算.
分析:根据题意,得四边形AODC的最小面积即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD=
 ,得其面积是
,得其面积是 ;要求最大面积,只需再进一步求得三角形DOC的面积,即是
;要求最大面积,只需再进一步求得三角形DOC的面积,即是 ,则最大面积是
,则最大面积是 .
.解答:
 解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.
解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.作CH⊥AO于H,
∵△AOC为等边三角形
∴CH=

∴S△AOC=
 ;
;当OD⊥OC时面积最大,
∴S△OCD=
 ,则最大面积是
,则最大面积是 +
+ =
=
∴四边形AODC的面积s的取值范围是
 <s≤
<s≤ .
.故选B.
点评:此题首先要能够正确分析出要求的四边形的最小面积和最大面积,然后根据等边三角形的性质以及三角形的面积公式进行计算.

练习册系列答案
相关题目
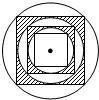 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 如图AOB是半径为1的单位圆的
如图AOB是半径为1的单位圆的
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是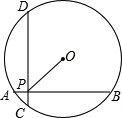

 D.
D.