题目内容
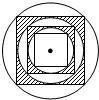
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是(
)nR
| ||
| 2 |
(
)nR
.
| ||
| 2 |
分析:由题意可得第一个的半径是R,△AOC是等腰直角三角形,则可求得第二个圆的半径,同理求得第三个圆的半径,继而可得规律:第n个圆的半径是(
)n-1R,又由第n个内切圆恰好是第n+1个圆,求得答案.
| ||
| 2 |
解答: 解:如图,连接OA,OB,OC,
解:如图,连接OA,OB,OC,
∵第一个的半径是R,△AOC是等腰直角三角形,
∴OC=
OA=
R,
即第二个圆的半径是
R,
同理,第三个圆的半径是(
)2R,
∴依此类推得到第n个圆,它的半径是(
)n-1R.
∵第n个内切圆恰好是第n+1个圆,
∴第n个内切圆,它的半径是(
)nR.
故答案为:(
)nR.
 解:如图,连接OA,OB,OC,
解:如图,连接OA,OB,OC,∵第一个的半径是R,△AOC是等腰直角三角形,
∴OC=
| ||
| 2 |
| ||
| 2 |
即第二个圆的半径是
| ||
| 2 |
同理,第三个圆的半径是(
| ||
| 2 |
∴依此类推得到第n个圆,它的半径是(
| ||
| 2 |
∵第n个内切圆恰好是第n+1个圆,
∴第n个内切圆,它的半径是(
| ||
| 2 |
故答案为:(
| ||
| 2 |
点评:此题考查了正多边形与圆的知识.此题难度适中,属于规律性题目,注意得到规律:第n个圆的半径是(
)n-1R是关键.
| ||
| 2 |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
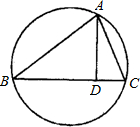 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6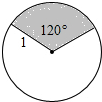 如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于
如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于