题目内容
如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离（45°）是1.5m，看旗杆顶部M的仰角为30°．两人相距23m且位于旗杆两侧（点B，N，D）在同一条直线上）．请求出旗杆MN的高度．（参考数据：
，
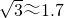，结果保留整数）
解：过点A作AE⊥MN于E，过点C作CF⊥MN于F，则EF=AB-CD=1.7-1.5=0.2
在Rt△AEM中，∠AEM=90°，∠MAE=45°
则AE=ME
设AE=ME=x
则MF=x+0.2，FC=23-x
在Rt△MFC中，∠MFC=90°，∠MCF=30°
则MF=CF•tan∠MCF，
则
解得x≈8.2
故MN=8.2+1.7≈10米
答：旗杆高约为10米．
分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形，应利用其公共边构造三角关系，进而可求出答案．
点评：本题考查了解直角三角形的问题．该题是一个比较常规的解直角三角形问题，建立模型比较简单，但求解过程中涉及到根式和小数，算起来麻烦一些．
练习册系列答案
阅读快车系列答案
相关题目
如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，看旗杆顶部M的仰角为30度．两人相距28米且位于旗杆两侧（点B，N，D在同一条直线上）．请求出旗杆MN的高度．（参考数据：
（2012•高邮市二模）如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离（45°）是1.5m，看旗杆顶部M的仰角为30°．两人相距23m且位于旗杆两侧（点B，N，D）在同一条直线上）．请求出旗杆MN的高度．（参考数据：
如图，某数学兴趣小组进行测量学校旗杆高度的数学活动，甲、乙两人分别站在旗杆的东、西两侧相距80m的点A、B处，利用测角仪在标杆顶端D、E处侧得旗杆顶端C的仰角分别为30°、55°，测角仪距地面1.6m．求学校旗杆CF的高度（精确到0.1m）（参考数据sin55°≈0.81，cos55°≈0.57，tan55°≈1.42，