��Ŀ����
����Ŀ��Ϊ�ˡ������������У�������������������ij������Ͻ���ڵ�һ�����Ϊ![]() �Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ
�Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ![]() ���ֲ��������
���ֲ��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
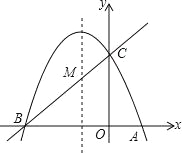
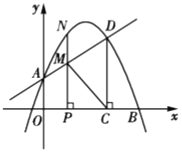
�ĺ�����ϵʽΪ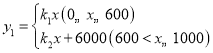 �������ͼ����ͼ��ʾ.�Ի��������
�������ͼ����ͼ��ʾ.�Ի��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() .
.
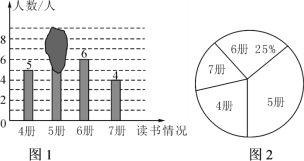
��1�����![]() ��
��![]() ��ֵ��
��ֵ��
��2�����ֻ������С��![]() ʱ���̻��ܷ���Ϊ
ʱ���̻��ܷ���Ϊ![]() ��Ԫ����д��
��Ԫ����д��![]() ��
��![]() �ĺ�����ϵʽ��������̻��ܷ���
�ĺ�����ϵʽ��������̻��ܷ���![]() �����ֵ.
�����ֵ.
���𰸡���1��![]() ��
��![]() ����2��
����2��![]()
![]() ���̻��ܷ���
���̻��ܷ���![]() �����ֵΪ32500Ԫ.
�����ֵΪ32500Ԫ.
��������
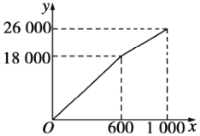
��1����x=600��y=18000����y1=k1x�ɵ�k1����x=1000��y=26000����y1=k2x+6000�ɵ�k2��
��2�������ֻ������С��![]() �����ֲ����С�ڵ���
�����ֲ����С�ڵ���![]() �������ܷ���=�ֲݵķ���+�ֻ��ķ����г����κ�������ʽ��Ȼ�����ݶ��κ��������ʿɵã�
�������ܷ���=�ֲݵķ���+�ֻ��ķ����г����κ�������ʽ��Ȼ�����ݶ��κ��������ʿɵã�
�⣺��1����ͼ���֪����![]() ��
��![]() �ϣ�����ã�
�ϣ�����ã�![]() ��
��
���![]() ��
��
��ͼ���֪����![]() ��
��![]() �ϣ�
�ϣ�
���![]() ��
��
��2�����ֻ������С��![]() ��
��
���ֲ����С�ڵ���![]() ��
��
������ɵã�
![]()
![]()
![]() ��
��
����![]() ʱ��
ʱ��![]() �����ֵΪ32500Ԫ.
�����ֵΪ32500Ԫ.
���̻��ܷ���![]() �����ֵΪ32500Ԫ..
�����ֵΪ32500Ԫ..

��ϰ��ϵ�д�
 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
�����Ŀ