题目内容
 (2012•西城区二模)在平面直角坐标系xOy中,A为第一象限内的双曲线y=
(2012•西城区二模)在平面直角坐标系xOy中,A为第一象限内的双曲线y=| k1 |
| x |
的横坐标为1,过点A作平行于 y轴的直线,与x轴交于点B,与双曲线y=
| k2 |
| x |
(1)当m=4时,求△ACD的面积(用含k1,k2的代数式表示);
(2)若点E恰好在双曲线y=
| k1 |
| x |
(3)设线段EB的延长线与y轴的负半轴交于点F,当点D的坐标为D(2,0)时,若△BDF的面积为1,且CF∥AD,求k1的值,并直接写出线段CF的长.
分析:(1)由于A、C的横坐标相同,则AC的长即为A、C的纵坐标之差,根据m=4,可求出BD的长,进而的得出三角形的面积;
(2)作EG⊥x轴于点G,判断出△DEG∽△DAB,再根据A,B,D三点的坐标分别为A(1,k1),B(1,0),D(m,0),以及G为BD的中点,求出E的表达式,代入反比例函数解析式,即可求出m的值;
(3)根据S△BDF=1,求出OF=2,将点B,点E的坐标分别代入解析式,求出直线BE的解析式为y=k1x-k1.再求出AD的解析式,根据平行直线的性质求出FC的解析式,得到C点作标,从而求出F从的坐标.
(2)作EG⊥x轴于点G,判断出△DEG∽△DAB,再根据A,B,D三点的坐标分别为A(1,k1),B(1,0),D(m,0),以及G为BD的中点,求出E的表达式,代入反比例函数解析式,即可求出m的值;
(3)根据S△BDF=1,求出OF=2,将点B,点E的坐标分别代入解析式,求出直线BE的解析式为y=k1x-k1.再求出AD的解析式,根据平行直线的性质求出FC的解析式,得到C点作标,从而求出F从的坐标.
解答: 解:(1)由题意得A,C两点的坐标分别为A(1,k1),C(1,k2).(如图1)
解:(1)由题意得A,C两点的坐标分别为A(1,k1),C(1,k2).(如图1)
∵k1>0,k2<0,
∴点A在第一象限,点C在第四象限,AC=k1-k2.
当m=4时,S△ACD=
AC•BD=
(k1-k2).
(2)作EG⊥x轴于点G.(如图2)
∵EG∥AB,AD的中点为E,
∴△DEG∽△DAB,
=
=
=
,G为BD的中点.
∵A,B,D三点的坐标分别为A(1,k1),B(1,0),D(m,0),
∴EG=
=
,BG=
=
,OG=OB+BG=
.
∴点E的坐标为E(
,
).
∵点E恰好在双曲线y=
上,
∴
•
=k1.①
∵k1>0,
∴方程①可化为
=1,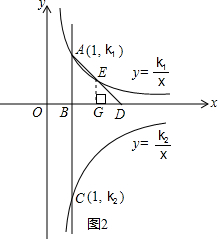
解得m=3.
(3)当点D的坐标为D(2,0)时,由(2)可知点E的坐标为E(
,
).(如图3)
∵S△BDF=1,
∴S△BDF=
BD•OF=
OF=1.
∴OF=2.
设直线BE的解析式为y=ax+b(a≠0).
∵点B,点E的坐标分别为B(1,0),E(
,
),
∴
解得 a=k1,b=-k1.
∴直线BE的解析式为y=k1x-k1.
∵线段EB的延长线与y轴的负半轴交于点F,k1>0,
∴点F的坐标为F(0,-k1),OF=k1.
∴k1=2.
∵A点坐标为(1,2),D点坐标为(2,0),
∴设一次函数解析式为y=kx+b,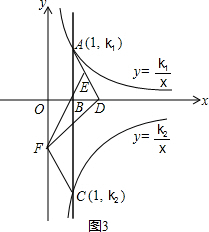
将A(1,2),D(2,0)分别代入解析式得,
,
解得
,
故函数解析式为y=-2x+4,
又∵AD∥FC,
设FC的解析式为y=-2x+c,
将F(0,-2)代入解析式得,c=-2,
故函数解析式为y=-2x-2.
当x=1时,k2=-4.
C点坐标为(1,-4),
故线段CF=
=
.
 解:(1)由题意得A,C两点的坐标分别为A(1,k1),C(1,k2).(如图1)
解:(1)由题意得A,C两点的坐标分别为A(1,k1),C(1,k2).(如图1)∵k1>0,k2<0,
∴点A在第一象限,点C在第四象限,AC=k1-k2.
当m=4时,S△ACD=
| 1 |
| 2 |
| 3 |
| 2 |
(2)作EG⊥x轴于点G.(如图2)
∵EG∥AB,AD的中点为E,
∴△DEG∽△DAB,
| EG |
| AB |
| DG |
| DB |
| DE |
| DA |
| 1 |
| 2 |
∵A,B,D三点的坐标分别为A(1,k1),B(1,0),D(m,0),
∴EG=
| AB |
| 2 |
| k1 |
| 2 |
| BD |
| 2 |
| m-1 |
| 2 |
| m+1 |
| 2 |
∴点E的坐标为E(
| m+1 |
| 2 |
| k1 |
| 2 |
∵点E恰好在双曲线y=
| k1 |
| x |
∴
| m+1 |
| 2 |
| k1 |
| 2 |
∵k1>0,
∴方程①可化为
| m+1 |
| 4 |

解得m=3.
(3)当点D的坐标为D(2,0)时,由(2)可知点E的坐标为E(
| 3 |
| 2 |
| k1 |
| 2 |
∵S△BDF=1,
∴S△BDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OF=2.
设直线BE的解析式为y=ax+b(a≠0).
∵点B,点E的坐标分别为B(1,0),E(
| 3 |
| 2 |
| k1 |
| 2 |
∴
|
解得 a=k1,b=-k1.
∴直线BE的解析式为y=k1x-k1.
∵线段EB的延长线与y轴的负半轴交于点F,k1>0,
∴点F的坐标为F(0,-k1),OF=k1.
∴k1=2.
∵A点坐标为(1,2),D点坐标为(2,0),
∴设一次函数解析式为y=kx+b,

将A(1,2),D(2,0)分别代入解析式得,
|
解得
|
故函数解析式为y=-2x+4,
又∵AD∥FC,
设FC的解析式为y=-2x+c,
将F(0,-2)代入解析式得,c=-2,
故函数解析式为y=-2x-2.
当x=1时,k2=-4.
C点坐标为(1,-4),
故线段CF=
| 12+(-4+2)2 |
| 5 |
点评:本题考查了反比例函数的相关问题,涉及图形与坐标的关系、待定系数法求函数解析式、两点间的距离公式等知识,综合性很强,要认真对待.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2012•西城区二模)如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若
(2012•西城区二模)如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若 (2012•西城区二模)如图,AB为⊙O的弦,半径OC⊥AB于点D,若OB长为10,cos∠BOD=
(2012•西城区二模)如图,AB为⊙O的弦,半径OC⊥AB于点D,若OB长为10,cos∠BOD=