题目内容
如图，点C，D在线段BF上，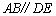
，
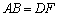，BC=DE．
求证：AC=FE．
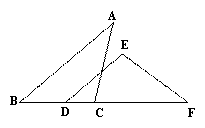
证明：∵ AB∥DE
∴ ∠B = ∠EDF；
在△ABC和△FDE中：
……………………………………3分
∴△A
BC≌△FDE(ASA)，………………………………………………4分
∴AC=FE. ………………………………………………………………5分
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
00007克，用科学记数法表示此数正确的是（ ）
B. 
C. 
D. 
销售量y（个）与它的定价x（元/个）的关系如图所示：
阅读理解：
学习了三角形全等的判定方法:“SAS”，“ASA”，“AAS”，“SSS”和直角三角形全等的判定方法“HL”后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究．
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠A=∠D.
初步探究：
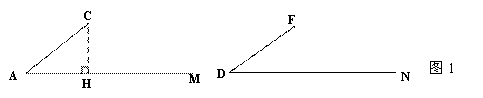
如图1，已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H，对△ABC 的CB边进行分类，可分为“CB<CH，CB=CH，CH<CB<CA，”三种情况进行探究．
 |
深入探究：
第一种情况，当BC<CH时，不能构成△ABC和△DEF．
第二种情况，（1）如图2，当BC=CH时，在△ABC和△DEF中，AC=DF，BC=EF，∠A=∠D，根据 ，可以知道Rt△ABC≌Rt△DEF．
 |
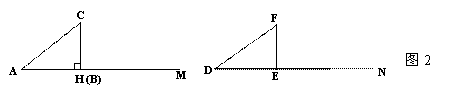第三种情况，（2）当CH<BC<CA时，△ABC和△DEF不一定全等．请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等（表明字母，不写作法，保留作图痕迹）．
（3）从上述三种情况发现，只有当BC=CH时，才一定能使△ABC≌△DEF． 除了上述三种情况外，BC边还可以满足什么条件，也一定能使△ABC≌△DEF？写出结论,并利用备用图证明.
 |
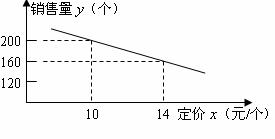
满足
。