题目内容
如图,在反比例函数y= (x>0)的图象经过点A,B(点A在B的上方).过点A分
(x>0)的图象经过点A,B(点A在B的上方).过点A分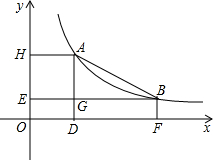 别作AD⊥x轴,AH⊥y轴,垂足分别为D,H;过点B分别作BF⊥x轴,BE⊥y轴,垂足分别为E,F,AD与BE交于点G.
别作AD⊥x轴,AH⊥y轴,垂足分别为D,H;过点B分别作BF⊥x轴,BE⊥y轴,垂足分别为E,F,AD与BE交于点G.
①比较大小:S四边形AHOD________S四边形BEOF;(填“>,=,<”)
②若OD:DG=2:1,则AG:BG=________.
= 1:2
分析:①由反比例函数的k的几何意义,可得S四边形AHOD=k,S四边形BEOF=k,继而求得答案;
②首先设OD=2a,DG=a,易得点A的坐标为:(2a, ),点B的坐标为:(
),点B的坐标为:( ,a),则可求得AG与BG的长,继而求得答案.
,a),则可求得AG与BG的长,继而求得答案.
解答:①∵反比例函数y= (x>0)的图象经过点A,B,AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,
(x>0)的图象经过点A,B,AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,
∴S四边形AHOD=k,S四边形BEOF=k,
∴S四边形AHOD=S四边形BEOF;
②∵OD:DG=2:1,
∴设OD=2a,DG=a,
∵AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,
∴四边形ADOH,OEBF,OEGD是矩形,
∴BF=DG=a,
∴点A的坐标为:(2a, ),点B的坐标为:(
),点B的坐标为:( ,a),
,a),
∴AD= ,BE=
,BE= ,
,
∴AG=AD-DG= -a=
-a=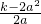 ,BG=BE-EG=
,BG=BE-EG= -2a=
-2a=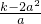 ,
,
∴AG:BG=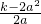 :
: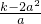 =1:2.
=1:2.
故答案为:(1)=,(2)1:2.
点评:此题考查了反比例函数的k的几何意义以及点与反比例函数的关系.此题难度适中,注意数形结合思想与方程思想的应用.
分析:①由反比例函数的k的几何意义,可得S四边形AHOD=k,S四边形BEOF=k,继而求得答案;
②首先设OD=2a,DG=a,易得点A的坐标为:(2a,
 ),点B的坐标为:(
),点B的坐标为:( ,a),则可求得AG与BG的长,继而求得答案.
,a),则可求得AG与BG的长,继而求得答案.解答:①∵反比例函数y=
 (x>0)的图象经过点A,B,AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,
(x>0)的图象经过点A,B,AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,∴S四边形AHOD=k,S四边形BEOF=k,
∴S四边形AHOD=S四边形BEOF;
②∵OD:DG=2:1,
∴设OD=2a,DG=a,
∵AD⊥x轴,AH⊥y轴,BF⊥x轴,BE⊥y轴,
∴四边形ADOH,OEBF,OEGD是矩形,
∴BF=DG=a,
∴点A的坐标为:(2a,
 ),点B的坐标为:(
),点B的坐标为:( ,a),
,a),∴AD=
 ,BE=
,BE= ,
,∴AG=AD-DG=
 -a=
-a=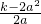 ,BG=BE-EG=
,BG=BE-EG= -2a=
-2a=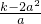 ,
,∴AG:BG=
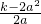 :
: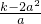 =1:2.
=1:2.故答案为:(1)=,(2)1:2.
点评:此题考查了反比例函数的k的几何意义以及点与反比例函数的关系.此题难度适中,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
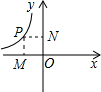 如图,在反比例函数
如图,在反比例函数 ,S2,…,Sn,则Sn=
,S2,…,Sn,则Sn=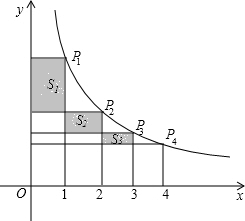 如图,在反比例函数y=
如图,在反比例函数y= n,求:
n,求: (2012•瑞安市模拟)如图,在反比例函数
(2012•瑞安市模拟)如图,在反比例函数