题目内容
解下列方程
(1)(3x-1)2=4(x+2)2
(2)2x2-3x+1=0
(3)x2-4x-6=0(用配方法求解)
(1)(3x-1)2=4(x+2)2
(2)2x2-3x+1=0
(3)x2-4x-6=0(用配方法求解)
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)开方,即可得出两个一元一次方程,求出方程的解即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答:解:(1)开方得:3x-1=±2(x+2),
解得:x1=5,x2=-
;
(2)分解因式得:(2x-1)(x-1)=0,
2x-1=0,x-1=0,
x1=
,x2=1;
(3)移项得:x2-4x=6,
配方得:x2-4x+4=6+4,
(x-2)2=10,
x-2=±
,
x1=2+
,x2=2-
.
解得:x1=5,x2=-
| 3 |
| 5 |
(2)分解因式得:(2x-1)(x-1)=0,
2x-1=0,x-1=0,
x1=
| 1 |
| 2 |
(3)移项得:x2-4x=6,
配方得:x2-4x+4=6+4,
(x-2)2=10,
x-2=±
| 10 |
x1=2+
| 10 |
| 10 |
点评:本题考查了解一元二次方程的应用,主要考查学生的解方程的能力,题目比较好,难度适中.

练习册系列答案
相关题目
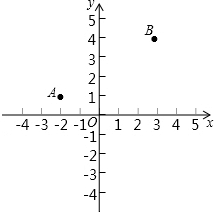 如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4).
如图,点A、B在平面直角坐标系的x轴的上方,其坐标为A(-2,1)、B(3,4).