题目内容
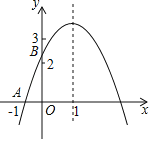
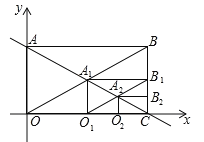
【题目】如图，直线y=﹣
x+2与x轴y轴分别交于A、C两点，以AC为对角线作第一个矩形ABCO，对角线交点为A1，再以CA1为对角线作第二个矩形A1B1CO1，对角线交点为A2，同法作第三个矩形A2B2CO2对角线交点为A3，…以此类推，则第2020个矩形对角线交点A2020的坐标为_____．
【答案】(2
﹣
，
)
【解析】
先根据矩形的性质以及相似三角形的判定定理证得：
，且相似比是（
）n，即可求得AnOn，OOn的长，进而确定An的坐标，即可求得A2020的坐标．
解：在y=﹣
x+2中
令x=0，解得：y=2；令y=0，解得：x=2.
∴则OC=2,OA=2.
∵A1是矩形ABCO的对角线的交点，O1A1//OA，
∴
，相似比为，
同理：
，相似比是（ ）n；
∴
∴
∴An的坐标为
∴A2020的坐标为(2﹣，)
练习册系列答案
相关题目
