��Ŀ����
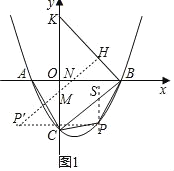
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��![]() x2��
x2��![]() x��4��x����A��B���㣬��y���ڵ�C.
x��4��x����A��B���㣬��y���ڵ�C.
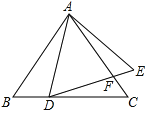
(1)��PΪ�߶�BC�·��������ϵ�����һ�㣬һ����G�ӵ�P�������ʵ�·����ÿ��1����λ�����˶���y����һ��M�������ʵ�·����ÿ��1����λ�����˶���x���ϵĵ�N������x����ÿ��![]() ����λ�����˶�����B.���ı���ACPB������ʱ�����˶�ʱ��t����Сֵ��
����λ�����˶�����B.���ı���ACPB������ʱ�����˶�ʱ��t����Сֵ��
(2)����C��AC�Ĵ��߽�x���ڵ�D������AOC�Ƶ�O��ת����ת���A��C�Ķ�Ӧ��ֱ�ΪA1��C1������ת������ֱ��A1C1��x�ύ�ڵ�Q.���߶�CD���ڵ�I.����DQI�ǵ���������ʱ��ֱ��д��DQ�ij���.

���𰸡�(1)t����СֵΪ![]() ��(2)DQ�ij���Ϊ
��(2)DQ�ij���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��������
(1)����B��BK��BC��y���ڵ�K����P��H��BK��BK�ڵ�H����y���ڵ�M����x���ڵ�N�����ʱ�˶���ʱ����С��������⣻
(2)����AOC�Ƶ�O��ת���൱�ڴ���һ���뾶ΪORԲO����������ת�����У�ACʼ��Ϊ��ֱ��OR�����ߣ�ȷ��Բ�İ뾶OR��OR����x�ᡢy�����ִ�������ֱ����ĸ����������⼴��.
�⣺(1)��PS��y�ύBC��S��
y��![]() x2��
x2��![]() x��4����x��0����y����4����y��0����x��-3��4��
x��4����x��0����y����4����y��0����x��-3��4��
�ʵ�A��B��C������ֱ�Ϊ(��3��0)��(4��0)��(0����4)��
��ֱ��BC�ı���ʽΪ��y��x��4��
S�ı���ACPB��S��ABC+S��PBC��
��S��ABC������
��ֻҪS��PBCȡ�����ֵ���ı���ACPB�����Ϊ���
���P(x��![]() x2��
x2��![]() x��4)�����S(x��x��4)��
x��4)�����S(x��x��4)��
S��PBC��![]() ��PS��OB��
��PS��OB��![]() ��4��(x��4��
��4��(x��4��![]() x2+
x2+![]() x+4)��
x+4)��![]() x2+
x2+![]() x��
x��
��![]() <0����S��PBC�����ֵ�����ı���ACPB��������ֵ��
<0����S��PBC�����ֵ�����ı���ACPB��������ֵ��
��ʱ��x��2���ʵ�P(2����![]() ).
).
����P����y��ĶԳƵ�P��(��2����![]() )��
)��
����B��BK��BC��y���ڵ�K����P��H��BK��BK�ڵ�H����y���ڵ�M����x���ڵ�N��
���ʱ�˶���ʱ����С��
t��P��M+MN+![]() BN��PM+MN+HN��
BN��PM+MN+HN��
ֱ��BK��BC����ֱ��BK�ı���ʽΪ��y����x+b��
����B�����������ʽ����ã�
ֱ��BK�ı���ʽΪ��y����x+4������
ͬ���ɵ�ֱ��P��H�ı���ʽΪ��y��x��![]() ������
������
�����٢�����ã�x��![]() ��
��
�ʵ�H(![]() ��
��![]() )��
)��
��t��P��H��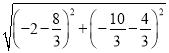 ��
��![]() ��
��
���˶�ʱ��t����СֵΪ![]() ��
��
(2)��AC��AD��
��ֱ��CD�ı���ʽΪ��y��![]() x��4��
x��4��
�ʵ�D(![]() ��0)��
��0)��
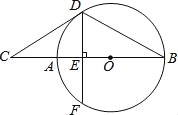
��ͼ2������O��OR��AC�ڵ�R��
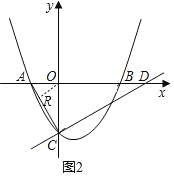
�������ʽ�ã�![]() OR��AC��
OR��AC��![]() OA��OC��
OA��OC��
����OR��![]() ��
��![]() ��
��
����ODC��������tan����![]() ��sin����
��sin����![]() ��
��
��tan2����![]() ��tan
��tan![]() ��
��![]() (֤������ע)��
(֤������ע)��
���һ����OR����y��ʱ��
����OR��һ��������ʱ����ͼ3��4��
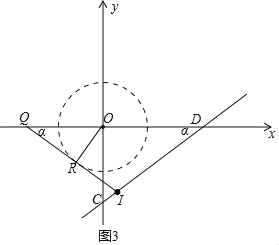
��ͼ3�У�IQ��ID��
��OQ��![]() ��
��![]() ��4��
��4��
��QD��![]() +4��
+4��![]() ��
��
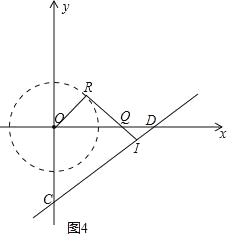
��ͼ4�У�IQ��ID��
ͬ��QD��![]() ��4��
��4��![]() ��
��
����OR�ڶ���������ʱ����ͼ5��6��
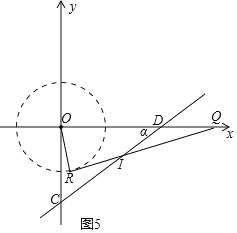
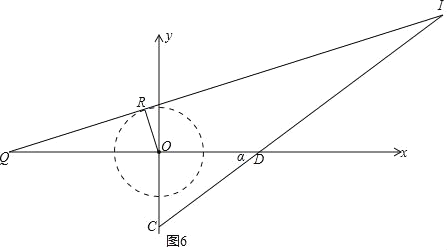
��ͼ5�У�DI��DQ��
����DQI����DIQ��![]() ��ODC��
��ODC��![]() ����
����
OQ��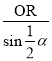 ��
��![]() ��
��
��DQ��![]() ��
��![]() ��
��
��ͼ6�У������߶�CD���ӳ����ཻ�����������⣻
���������OR����x��ʱ��
����ͼ������R�ڶ���������ʱ����ͼ7��
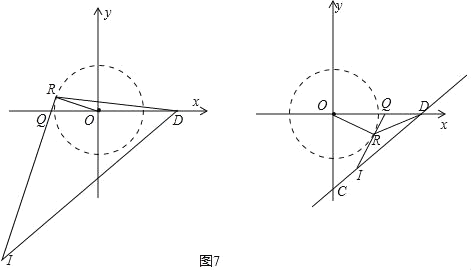
�����ͼ�������߶�DC���ӳ����ཻ�����������⣻
���Ҳ�ͼ��ͬ���ɵã�DQ��![]() ��
��![]() ��
��![]() ��
��
����R��һ��������ʱ����ͼ8��
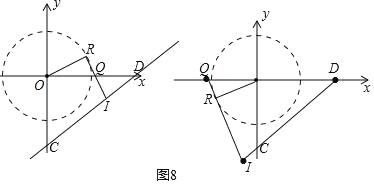
�����ͼ��ͬ���ɵã�DQ��![]() ��
��![]()
���Ҳ�ͼ�������߶�DC���ӳ����ཻ�����������⣻
����������DQ�ij���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() +
+![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��ע����֪tan����![]() ����tan2����tan
����tan2����tan![]() .
.
��ͼ��ABD����BDΪ�ĵ��������Σ�AC��BD������D��DH��AB��
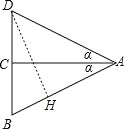
���裺��DAC����BAC������tan����![]() ����BC��CD��3a����AC��4a��
����BC��CD��3a����AC��4a��
�������ε������ʽ�ã�![]() AH��AB��
AH��AB��![]() DB��AC��
DB��AC��
��ã�AH��![]() ��
��![]() ��
��
��sin2����sin��BAD��![]() ��
��![]() ��tan2����
��tan2����![]() ��
��
ͬ���ɵã�tan![]()
![]() ��
��![]() .
.

����Ŀ�����ȵ���������֮��.Ϊ�˵�����Уѧ��������ȫ֪ʶˮƽ��ѧУ��֯��һ��ȫУ��������ȫ֪ʶ��ѵ����ѵ�����в��ԣ���ȫУ2400��ѧ���У��ֱ��ȡ��������Ů����15�ݳɼ������������������£��벹������.
���ռ����ݣ�
����15��ѧ�����Գɼ�ͳ�����£�
68��72��89��85��82��85��74��92��80��85��76��85��69��78��80
Ů��15��ѧ�����Գɼ�ͳ�����£�(����100��)
82��88��83��76��73��78��67��81��82��80��80��86��82��80��82
�����·����������������������������ݣ�
��� Ƶ�� | 65.5��70.5 | 70.5��75.5 | 75.5��80.5 | 80.5��85.5 | 85.5��90.5 | 90.5��95.5 |
���� | 2 | 2 | 4 | 5 | 1 | 1 |
�� | 1 | 1 | 5 | 6 | 2 | 0 |
���������ݣ�
(1)�����������ݵ�ƽ��������������λ�����������±���ʾ��
�༶ | ƽ���� | ���� | ��λ�� | ���� |
���� | 80 | x | 80 | 45.9 |
�� | 80 | 82 | y | 24.3 |
�ڱ��У�x��_____��y��_____.
(2)���涨�÷���80������(����80��)Ϊ�ϸ������ȫУѧ����������ȫ֪ʶ�ϸ��ѧ����______��.
(3)ͨ�����ݷ����õ��Ľ�����Ů������������ȫ���֪ʶ������ˮƽ�������ã������������˵������.