题目内容
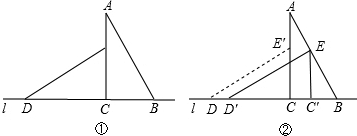
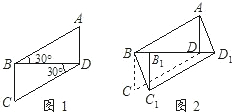
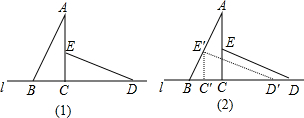
将两块全等的含30°角的三角尺如图1摆放在一起,它们的较短直角边长为3(1)将△ECD沿直线l向左平移到图2的位置,使E点落在AB上,点C平移后的对应点为C1,则CC1=______
【答案】分析:(1)根据题意:E1是AB的中点,即BC1=BC-CC1,则CC1=BC-BC1,进而求出即可,△ECD绕点C旋转的度数即∠ECE2的度数;易得:∠ECE2=∠BAC=30°;
(2)根据条件,由AAS证明△AEF≌△D1BF进而得出AF=FD1.
解答: 解:(1)∵EC=3,∠A=30°,
解:(1)∵EC=3,∠A=30°,
∴AC= =3
=3 ,
,
∴AE=3 -3,
-3,
∴CC1=EE1=AE×tan30°=3- ;
;
△ECD绕点C旋转的度数即∠ECE2的度数;
∵∠ABC=60°,BC=CE2=3,AB=6,
∴△E2BC是等边三角形,
∴BC=E2C=E2B=3,
∴AE2=E2C=3,
∴∠E2AC=∠E2CA,
∴∠ECE2=∠BAC=30°.
故答案为:3- ,30;
,30;
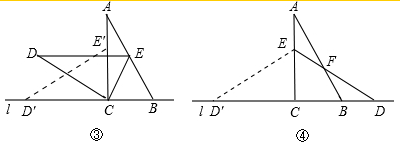
(2)证明:在△AEF和△D1BF中,
∵AE=AC-EC,D1B=D1C-BC,
又AC=D1 C,EC=BC,∴AE=D1 B.
∠D1BF=∠AEF=180°-60°=120°,
在△AEF和△D1BF中
∵ ,
,
∴△AEF≌△D1BF(AAS).
∴AF=F D1.
点评:本题考查平移、旋转的性质;平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.
(2)根据条件,由AAS证明△AEF≌△D1BF进而得出AF=FD1.
解答:
 解:(1)∵EC=3,∠A=30°,
解:(1)∵EC=3,∠A=30°,∴AC=
 =3
=3 ,
,∴AE=3
 -3,
-3,∴CC1=EE1=AE×tan30°=3-
 ;
;△ECD绕点C旋转的度数即∠ECE2的度数;
∵∠ABC=60°,BC=CE2=3,AB=6,
∴△E2BC是等边三角形,
∴BC=E2C=E2B=3,
∴AE2=E2C=3,
∴∠E2AC=∠E2CA,
∴∠ECE2=∠BAC=30°.
故答案为:3-
 ,30;
,30;(2)证明:在△AEF和△D1BF中,
∵AE=AC-EC,D1B=D1C-BC,
又AC=D1 C,EC=BC,∴AE=D1 B.
∠D1BF=∠AEF=180°-60°=120°,
在△AEF和△D1BF中
∵
 ,
,∴△AEF≌△D1BF(AAS).
∴AF=F D1.
点评:本题考查平移、旋转的性质;平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心.

练习册系列答案
相关题目
 活用知识,解决问题.
活用知识,解决问题.
 )的位置,使E点落在AB上,则CC′=( )
)的位置,使E点落在AB上,则CC′=( )