题目内容
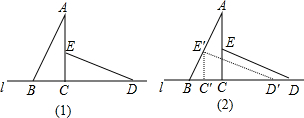
将两块全等的含30°角的三角尺如图①摆放在一起,它们的较短直角边长为6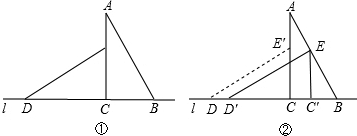
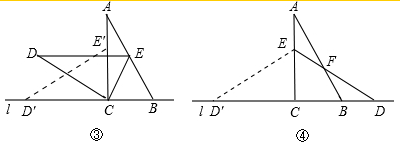
(1)将△DCE沿直线l向右平移到图②的位置,使E点落在AB上,则平移的距离CC′=
(2)将△DCE绕点C按顺时针方向旋转到图③的位置,使点E落在AB上,则△DCE旋转的度数=
(3)将△DCE沿直线AC翻折到图④的位置,ED′与AB相交于点F,求证:BF=EF.
分析:(1)根据三角函数求得AC的长,易证△BEC′∽△BAC,根据相似三角形对应边的比相等,即可求得BC′,则可得CC′的长;
(2)根据旋转的定义得到:CE=CB,易证△BCE是等边三角形,则∠BCE可得,则△DCE旋转的度数即可求解;
(3)证明△AEF≌△D′BF即可证得.
(2)根据旋转的定义得到:CE=CB,易证△BCE是等边三角形,则∠BCE可得,则△DCE旋转的度数即可求解;
(3)证明△AEF≌△D′BF即可证得.
解答:解:(1)在直角△ABC中,AC=BC•tan60°=6
.
∵△BEC′∽△BAC,
∴
=
即
=
,
解得:BC′=2
,
∴CC′=BC-BC′=6-2
;
(2)∵△BCE中,CE=CB,∠EBC=60°,
∴△BCE是等边三角形,
∴∠BCE=60°,
∴∠ACE=90-60=30°,即△DCE旋转的度数是30度.
(3)∵AC=CD′,CE=CB,
∴AE=BD′,
又∵∠AFE=∠D′FB,∠A=∠ED′C,
∴△AEF≌△D′BF,
∴BF=EF.
| 3 |
∵△BEC′∽△BAC,
∴
| BC′ |
| BC |
| C′E′ |
| AC |
| BC′ |
| 6 |
| 6 | ||
6
|
解得:BC′=2
| 3 |
∴CC′=BC-BC′=6-2
| 3 |
(2)∵△BCE中,CE=CB,∠EBC=60°,
∴△BCE是等边三角形,
∴∠BCE=60°,
∴∠ACE=90-60=30°,即△DCE旋转的度数是30度.
(3)∵AC=CD′,CE=CB,
∴AE=BD′,
又∵∠AFE=∠D′FB,∠A=∠ED′C,
∴△AEF≌△D′BF,
∴BF=EF.
点评:本题主要考查了旋转的定义,注意先确定旋转角,并且在证明线段相等的问题,一般是转化为证明三角形全等的问题来解决.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 活用知识,解决问题.
活用知识,解决问题.
 )的位置,使E点落在AB上,则CC′=( )
)的位置,使E点落在AB上,则CC′=( )