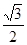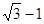Question

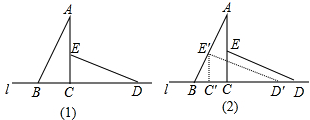
如图，将两块全等的含30°角的三角尺如图（1）摆放在一起，它们的较短直角边长为

3

． 将△ECD沿直线l向左平移到图（2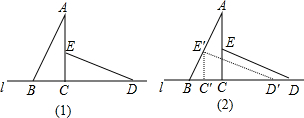）的位置，使E点落在AB上，则CC′=（　　）

• A．1
• B．

  3

  2

• C．

  3

  -1
• D．2-

  3

Answer 1

分析：根据平移的性质可知CC'为平移的距离，先求BC′的长度，进而可得平移的距离．

解答：解：根据平移的性质可知CC'为平移的距离．
∵在Rt△ABC中，BC=

3

，∠A=30°，
∴AB=2BC=2

3

，AC=3．
∵C′E′∥CE，
∴△BC′E′∽△BCA，
∴BC′：BC=E′C′：AC，
∴BC′=1，
∴CC′=

3

-1．
故选C．

点评：本题考查平移的性质；平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．