题目内容
已知：如图，AB是⊙O的直径，弦CD⊥AB于E，M为 |
| AB |
考点：圆周角定理,垂径定理,圆内接四边形的性质
专题：证明题
分析：连结BC，如图，先根据垂径定理得AC弧=AD弧，则利用圆周角定理得到∠ABC=∠AMD，再根据圆内接四边形的性质得∠FMC=∠ABC，所以∠AMD=∠FMC．
解答：
证明：连结BC，如图，
∵弦CD⊥直径AB，
∴AC弧=AD弧，
∴∠ABC=∠AMD，
∵∠FMC=∠ABC，
∴∠AMD=∠FMC．
证明：连结BC，如图，∵弦CD⊥直径AB，
∴AC弧=AD弧，
∴∠ABC=∠AMD，
∵∠FMC=∠ABC，
∴∠AMD=∠FMC．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理和圆内接四边形的性质．
练习册系列答案
相关题目
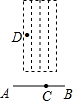如图，田径运动会上，七年级二班的小亮同学从点C起跳，假若落地点是D，且线段CD的长度是一定的，则当AB与CD
如图，已知A、B、C三点在⊙O上，AC⊥BO于D，∠B=53°，则∠BOC的度数是
下列三个图，均由4个完全相同的小正方形组合而成，分别添加一个相同的正方形，使它们成为不同的轴对称图形．
若代数式
的值是负数，则x的取值范围是（ ）
| 3 |
| 5x+2 |
A、x＜-
| ||
B、x＜-
| ||
C、x＞-
| ||
D、x＞-
|